题目内容
已知数列{xn}满足xn+3=xn，xn+2=|xn+1-xn|（n∈N*），x1=1，x2=a（a≤1，a≠0）则数列{xn}的前2010项的和S2010为 ．
考点：数列的求和
专题：点列、递归数列与数学归纳法
分析：由xn+3=xn，判断数列是周期数列，得到周期为3，求出一个周期的数值的和，然后求解数列{xn}的前2010项的和S2010．
解答：
解：因为数列{xn}满足xn+3=xn，xn+2=|xn+1-xn|（n∈N*），
若x1=1，x2=a（a≤1，a≠0），
所以x3=|a-1|=1-a，x4=x1=1，
所以数列是以3为周期的周期数列，
并且x1+x2+x3=1+1-a+a=2，
所以S2010=x1+x2+x3+…+xn=670（x1+x2+x3）=1340．
故答案为：1340
若x1=1，x2=a（a≤1，a≠0），
所以x3=|a-1|=1-a，x4=x1=1，
所以数列是以3为周期的周期数列，
并且x1+x2+x3=1+1-a+a=2，
所以S2010=x1+x2+x3+…+xn=670（x1+x2+x3）=1340．
故答案为：1340
点评：本题主要考查数列的求和，根据条件利用数列的周期性是解决本题的关键，注意一个周期的数值的和，考查计算能力．
练习册系列答案
相关题目
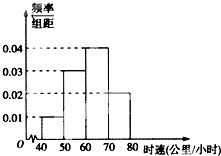已知某一段公路限速60公里/小时，现抽取200辆通过这一段公路的汽车的时速，其频率分布直方图如图所示，则这200辆汽车中在该路段没有超速的有