题目内容

已知正三棱锥的侧棱长是底面边长的2倍，则侧棱与底面所成角的余弦值为
 
．
考点：直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：首先利用正三棱锥的性质，设底面边长为AB=a，进一步求得侧棱长为：AC=2a，顶点A在下底面的射影为O点．利用勾股定理求得：DE=
3
a
2
，进一步求得：OD=
3
3
a，最后在Rt△AOD中，利用余弦公式求的结果．
解答： 解：正三棱锥的侧棱长是底面边长的2倍，如图，设底面边长为BC=a，
则：侧棱长为：AC=2a
顶点A在下底面的射影为O点．
利用勾股定理求得：DE=
3
a
2

进一步求得：OD=
3
3
a
在Rt△AOD中，cos∠ADO=
3
3
a
2a
=
3
6
点评：本题考查的知识要点：正三棱锥的性质，线面的夹角及相关的运算．
练习册系列答案
相关题目
已知函数f（x）=ax2+（a-1）x-1，有且仅有一个零点的充要条件是
 
．
在单位圆上，点P从（0，1）出发，沿单位圆x2+y2=1顺时针方向运动
2π
3
弧长到达Q点，则Q 点的坐标为（　　）
A、（-
1
2
，
3
2
）
B、（
3
2
，-
1
2
）
C、（
1
2
，-
3
2
）
D、（-
3
2
，-
1
2
）
下面四个命题：
①已知函数f（x）=sin x，在区间[0，π]上任取一点x0，则使得f（x0）＞
1
2
的概率为
2
3
；
②函数y=sin 2x的图象向左平移
π
3
个单位得到函数y=sin（2x+
π
3
）的图象；
③命题“?x∈R，x2-x+1≥
3
4
”的否定是“?x0∈R，x02-x0+1＜
3
4
”；
④若函数f（x）是定义在R上的奇函数，且f（x+4）=f（x），则f（2 012）=0．
向量
a
=（-1，1）在向量
b
=（3，4）方向上的投影为
1
5
．
其中所有正确命题的序号是
 
．
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3，则（　　）
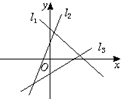
A、k1＜k2＜k3
B、k3＜k1＜k2
C、k3＜k2＜k1
D、k1＜k3＜k2
一个箱子里装有5个大小相同的球，有3个白球，2个红球，从中摸出2个球．
（1）求摸出的两个球中有1个白球和一个红球的概率；
（2）用ξ表示摸出的两个球中的白球个数，求ξ的分布列及数学期望．
已知命题p：?x∈R，使得x2+2ax+2-a=0成立，命题q：?x∈[0，1]，使得x+1＜a，若命题p且￢q为真命题，则实数a的取值范围是
 
．
已知函数f（x）=3x的反函数经过点（18，a+2），设g（x）=3ax-4x的定义域为区间[-1，1]，
（1）求g（x）的解析式；
（2）若方程g（x）=m有解，求m的取值范围；
（3）对于任意的n∈R，试讨论方程g（|x|）+2|x|+1=n的解的个数．
求（2-3×5-1）+（4-6×5-2）+（6-9×5-3）+…+（2n-3n×5-n）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网