题目内容
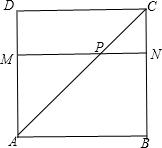
在边长为a的正方形ABCD中,M,N分别为DA、BC上的点,且MN∥AB,连结AC交MN于点P,现沿MN将正方形ABCD折成直二面角.
(1)求证:无论MN怎样平行移动(保持MN∥AB),∠APC的大小不变并求出此定值;
(2)当MN在怎样的位置时,M点到面ACD的距离最大?
(1)求证:无论MN怎样平行移动(保持MN∥AB),∠APC的大小不变并求出此定值;
(2)当MN在怎样的位置时,M点到面ACD的距离最大?
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)首先根据勾股定理求出相关的线段长,进一步利用余弦定理求得∠APCD的余弦值为定值.
(2)利用点到平面的距离,求出ME,进一步利用均值不等式求出结果.
(2)利用点到平面的距离,求出ME,进一步利用均值不等式求出结果.
解答:
(1)证明:在边长为a的正方形ABCD中,M,N分别为DA、BC上的点,且MN∥AB,连结AC交MN于点P,现沿MN将正方形ABCD折成直二面角.
设MC=x,(0<x<a)根据AC平分∠DAB得到:PN=x,MP=a-x,MA=a-x,AN=
,
AP=
(a-x)
PC=
x
进一步在△APC中利用余弦定理:cos∠APC=
=-
所以:无论MN怎样平行移动(保持MN∥AB),∠APC的大小不变.此定值为-
.
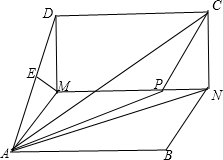
(2)由图形可知:MN∥平面ACD
过M作ME⊥平面ACD,设MD=x
利用面积相等得:ME=
=
≤
≤
=
(当且仅当x=
时)
即:当M在中点时,M点到面ACD的距离最大.
设MC=x,(0<x<a)根据AC平分∠DAB得到:PN=x,MP=a-x,MA=a-x,AN=
| a2+(a-x)2 |
AP=
| 2 |
PC=
| 2 |
进一步在△APC中利用余弦定理:cos∠APC=
| AP2+PC2-AC2 |
| 2AP•PC |
| 1 |
| 2 |
所以:无论MN怎样平行移动(保持MN∥AB),∠APC的大小不变.此定值为-
| 1 |
| 2 |
(2)由图形可知:MN∥平面ACD
过M作ME⊥平面ACD,设MD=x
利用面积相等得:ME=
| x(a-x) | ||
|
| 1 | ||||||
|
| ||
|
| ||
|
| ||
| 4 |
| a |
| 2 |
即:当M在中点时,M点到面ACD的距离最大.


点评:本题考查的知识要点:折叠问题在立体几何中的应用,余弦定理得应用,勾股定理得应用,均值不等式的应用及相关的运算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合M={2,4,6,8},N={1,2},P={x|x=
,a∈M,b∈N},则集合P的真子集的个数为( )
| a |
| b |
| A、4 | B、6 | C、15 | D、63 |
阅读如图所示的程序框图,运行相应的程序,若输入的值为9,则输出的值为( )


| A、1064 | B、1065 |
| C、1067 | D、1068 |