题目内容
求函数f(x)=
的最小值.
| 2xlnx |
| 1-x2 |
考点:函数的值域
专题:导数的综合应用
分析:先求出f(x)的导数,再令g(x)=lnx-
,对g(x)求导,得出f(x)的单调区间,得出f(1)是最小值,而x=1不在定义域,求极限即可.
| x2-1 |
| x2+1 |
解答:
解:∵f(x)=
,
∴f(x)=
,
令f′(x)=0,得:lnx=
,
设g(x)=lnx-
,
显然函数g(x)有一个零点x=1,
对函数g(x)求导得:
g′(x)=
-
=
≥0,
当且仅当x=1时等号成立,(x>0).
∴函数g(x)在其定义域上单调递增,
∴x=1为函数f(x)唯一驻点,
∵函数g(x)在x>0时单调递增,且在x=1时g(1)=0,
∴在(0,1)上,g(x)<0,f(x)单调递减;
在(1,+∞)上,g(x)>0,f(x)单调递增.
∴f(x)min=f(1),
很明显,f(x)的定义域不包含1,
故求出
f(x)即可,
由洛必达法则得:
f(x)=
=
=
(-lnx-1)
=-1.
| 2xlnx |
| 1-x2 |
∴f(x)=
| 2(1+x2)lnx+2(1-x2) |
| (1-x2)2 |
令f′(x)=0,得:lnx=
| x2-1 |
| x2+1 |
设g(x)=lnx-
| x2-1 |
| x2+1 |
显然函数g(x)有一个零点x=1,
对函数g(x)求导得:
g′(x)=
| 1 |
| x |
| 4x |
| (x2+1)2 |
=
| (x2-1)2 |
| x(x2+1)2 |
当且仅当x=1时等号成立,(x>0).
∴函数g(x)在其定义域上单调递增,
∴x=1为函数f(x)唯一驻点,
∵函数g(x)在x>0时单调递增,且在x=1时g(1)=0,
∴在(0,1)上,g(x)<0,f(x)单调递减;
在(1,+∞)上,g(x)>0,f(x)单调递增.
∴f(x)min=f(1),
很明显,f(x)的定义域不包含1,
故求出
| lim |
| x→1 |
由洛必达法则得:
| lim |
| x→1 |
| lim |
| x→1 |
| 2xlnx |
| 1-x2 |
=
| lim |
| x→1 |
| 2lnx+2 |
| -2x |
=
| lim |
| x→1 |
=-1.
点评:本题属于求函数的值域问题,利用导数求函数的单调区间,确定函数取最小值的x的范围,由于x=1不在定义域内,需用到洛必达法则.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知平面向量
=(a,0),
=(0,b),其中a,b为[-2,2]上的两个随机实数,定义平面上的点集Ω,Ω1,Φ分别为Ω={P|
=
+
},Ω1={Q|
|=|
|=
且|QP|<1,P∈Ω},Φ:Ω1∪{R|
<|
|<2}.若在Ω对应的平面区域内随机取一个点W,则点W落在Φ对应的平面区域内的概率为( )
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
已知命题p:y=cosx是偶函数,命题q:?x∈R,sinx=2,则下列判断正确的是( )
| A、¬p是真命题 |
| B、¬q是假命题 |
| C、p∧q是真命题 |
| D、¬p∨q是假命题 |
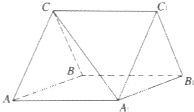 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.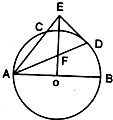 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.