题目内容
已知命题p：y=cosx是偶函数，命题q：?x∈R，sinx=2，则下列判断正确的是（ ）
| A、￢p是真命题 |
| B、￢q是假命题 |
| C、p∧q是真命题 |
| D、￢p∨q是假命题 |
考点：复合命题的真假
专题：规律型
分析：本题考查的知识点是复合命题的真假判定，解决的办法是先判断组成复合命题的简单命题的真假，再根据真值表进行判断．
解答：
解：∵y=cosx是偶函数，
∴命题p为真命题；
∵对于?x∈R，都有sinx≤1，
∴命题q为假命题，
∴￢p为假命题，
∴￢p∨q是假命题
故选：D．
∴命题p为真命题；
∵对于?x∈R，都有sinx≤1，
∴命题q为假命题，
∴￢p为假命题，
∴￢p∨q是假命题
故选：D．
点评：本题看出命题真假的判断，本题解题的关键是先判断出条件中所给的两个命题的真假，本题是一个基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
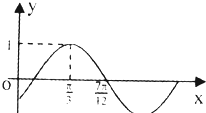已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
设等差数列{an}的公差为d，前n项和为Sn．若a1=d=1，则
的最小值为（ ）
| Sn+8 |
| an |
| A、10 | ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）=（x-1）[x2+（a+1）x+a+b+1]的三个零点值分别可以作为抛物线、椭圆、双曲线的离心率，则a2+b2的取值范围是（ ）
A、[
| ||
B、（
| ||
| C、[5，+∞） | ||
| D、（5，+∞） |