题目内容
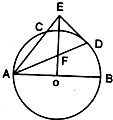 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.考点:圆的切线的判定定理的证明
专题:选作题,立体几何
分析:连接OD,△AOD是等腰三角形,结合,∠BAC的平分线AD,得到OD∥AE可得结论.
解答:
 证明:连接OD,
证明:连接OD,
∵OD=OA,
∴∠OAD=∠ADO,
∵∠EAD=∠BAD,
∴∠EAD=∠ADO,
∴OD∥AE,
∴∠AED+∠ODE=180°,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
 证明:连接OD,
证明:连接OD,∵OD=OA,
∴∠OAD=∠ADO,
∵∠EAD=∠BAD,
∴∠EAD=∠ADO,
∴OD∥AE,
∴∠AED+∠ODE=180°,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
点评:考查了切线的判定定理,能够综合运用角平分线的性质以及平行线分线段成比例定理.

练习册系列答案
相关题目
已知P、M、N是单位圆上互不相同的三个点,且满足|
|=|
|,则
•
的最小值是 ( )
| PM |
| PN |
| PM |
| PN |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
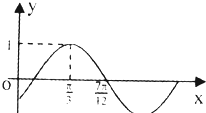 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|

 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为