题目内容
在平面直角坐标系中,点P是不等式组
所确定的平面区域内的动点,Q是直线2x+y=0上的任意一点,O为坐标原点,则|
+
|的最小值为 .
|
| OP |
| OQ |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用数形结合,结合向量的基本运算即可得到结论.
解答:
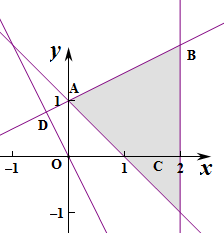 解:作出不等式组对应的平面区域:
解:作出不等式组对应的平面区域:
设P(x,y),
∵Q在直线2x+y=0上,
∴设Q(a,-2a),
则
+
=(x+a,y-2a),
则|
+
|=
,
设z=|
+
|=
,
则z的几何意义为平面区域内的动点P到动点Q的距离的最小值,
由图象可知当P位于点A(0,1)时,
Q为P在直线2x+y=0的垂足时,
z取得最小值为d=|AD|=
=
=
,
故答案为:
.
 解:作出不等式组对应的平面区域:
解:作出不等式组对应的平面区域:设P(x,y),
∵Q在直线2x+y=0上,
∴设Q(a,-2a),
则
| OP |
| OQ |
则|
| OP |
| OQ |
| (x+a)2+(y-2a)2 |
设z=|
| OP |
| OQ |
| (x+a)2+(y-2a)2 |
则z的几何意义为平面区域内的动点P到动点Q的距离的最小值,
由图象可知当P位于点A(0,1)时,
Q为P在直线2x+y=0的垂足时,
z取得最小值为d=|AD|=
| |1| | ||
|
| 1 | ||
|
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:本题主要考查线性规划的应用,利用平面向量的基本运算,利用数形结合是解决本题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知函数f(x)=(x-1)[x2+(a+1)x+a+b+1]的三个零点值分别可以作为抛物线、椭圆、双曲线的离心率,则a2+b2的取值范围是( )
A、[
| ||
B、(
| ||
| C、[5,+∞) | ||
| D、(5,+∞) |
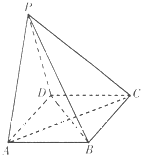 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD= 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为