题目内容
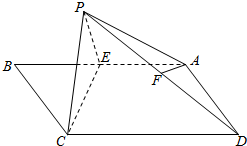 如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.
如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)当∠PEB=60°时,
①求证:平面PCE⊥平面AECD;
②求PD与平面AECD所成角的正切值.
考点:直线与平面平行的判定,直线与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取DC中点G,连结GF,AG,由G,F为中点,判断出FG∥PC,根据线面平行的判定定理知FG∥平面PCE,由AE=CG,AE∥CG,推知四边形AECG为平行四边形,进而可知AG∥CE,利用线面平行的判定定理推断出AG∥平面PCE,则根据面面平行的判定定理可知平面AFG∥平面PCE,利用面面平行的性质可推断出AF∥平面PCE.
(Ⅱ)①由∠PEB=60°,PE=BE=1,推断出PB=1,取CE的中点O,PE=PC=1,且∠EPC=90°,求得OP,同理可求得OB,进而知OP2+OB2=BP2,判断出OP⊥OB,又有OP⊥CE,CE?平面BEC,OB?平面BEC,BO∩OP=P,推断出OP⊥平面BEC,即OP⊥平面CDEF,最后根据线面垂直的判定定理推断出平面PCE⊥平面AECD.
②连结OD,OP⊥平面CDEF,进而可知∠PDO为PD与平面AECD所成角,由BE=CE,∠B=90°,求得∠ECB=45°,进而可知∠ECD=45°,利用余弦定理求得OD,则tan∠PDO可求得.
(Ⅱ)①由∠PEB=60°,PE=BE=1,推断出PB=1,取CE的中点O,PE=PC=1,且∠EPC=90°,求得OP,同理可求得OB,进而知OP2+OB2=BP2,判断出OP⊥OB,又有OP⊥CE,CE?平面BEC,OB?平面BEC,BO∩OP=P,推断出OP⊥平面BEC,即OP⊥平面CDEF,最后根据线面垂直的判定定理推断出平面PCE⊥平面AECD.
②连结OD,OP⊥平面CDEF,进而可知∠PDO为PD与平面AECD所成角,由BE=CE,∠B=90°,求得∠ECB=45°,进而可知∠ECD=45°,利用余弦定理求得OD,则tan∠PDO可求得.
解答:

(Ⅰ)证明:取DC中点G,连结GF,AG,
∵G,F为中点,
∴FG∥PC,
∵PC?平面PCE,FG?平面PCE,
∴FG∥平面PCE,
∵AE=CG,AE∥CG,
∴四边形AECG为平行四边形,
∴AG∥CE,
∵CE?平面PCE,AG?平面PCE,
∴AG∥平面PCE,
∵AG?平面AFG,FG?平面AFG,FG∩AG=G,
∴平面AFG∥平面PCE,
∵AF?平面AFG,
∴AF∥平面PCE.
(Ⅱ)①证明:∵∠PEB=60°,PE=BE=1,
PB=1,取CE的中点O,
∵PE=PC=1,且∠EPC=90°,
∴OP=
,同理可求得OB=
,
∴OP2+OB2=BP2,
∴OP⊥OB,
∵OP⊥CE,CE?平面BEC,OB?平面BEC,BO∩OP=P,
∴OP⊥平面BEC,即OP⊥平面CDEF,
∵OP?平面PCE,
∴平面PCE⊥平面AECD.
②连结OD,∵OP⊥平面CDAF,
∴∠PDO为PD与平面AECD所成角,
∵BE=CE,∠B=90°,
∴∠ECB=45°,
∴∠ECD=45°,
∴OD=
=
∴tan∠PDO=
=
×
=
.

(Ⅰ)证明:取DC中点G,连结GF,AG,
∵G,F为中点,
∴FG∥PC,
∵PC?平面PCE,FG?平面PCE,
∴FG∥平面PCE,
∵AE=CG,AE∥CG,
∴四边形AECG为平行四边形,
∴AG∥CE,
∵CE?平面PCE,AG?平面PCE,
∴AG∥平面PCE,
∵AG?平面AFG,FG?平面AFG,FG∩AG=G,
∴平面AFG∥平面PCE,
∵AF?平面AFG,
∴AF∥平面PCE.
(Ⅱ)①证明:∵∠PEB=60°,PE=BE=1,
PB=1,取CE的中点O,
∵PE=PC=1,且∠EPC=90°,
∴OP=
| ||
| 2 |
| ||
| 2 |
∴OP2+OB2=BP2,
∴OP⊥OB,
∵OP⊥CE,CE?平面BEC,OB?平面BEC,BO∩OP=P,
∴OP⊥平面BEC,即OP⊥平面CDEF,
∵OP?平面PCE,
∴平面PCE⊥平面AECD.
②连结OD,∵OP⊥平面CDAF,
∴∠PDO为PD与平面AECD所成角,
∵BE=CE,∠B=90°,
∴∠ECB=45°,
∴∠ECD=45°,
∴OD=
| CD2+OC2-2CD•OC•cos45° |
| ||
| 2 |
∴tan∠PDO=
| OP |
| OD |
| ||
| 2 |
| 2 | ||
|
| ||
| 5 |
点评:本题主要考查了线面垂直,线面平行以及面面垂直的判定定理,线与面所成的角问题.在解决二面角或线面角的时候,关键是找到平面角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,x∈R,a≤x4-4x3+4x2+1恒成立,则a的最大值为( )
| A、0 | B、1 | C、2 | D、3 |
 如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4,
如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4, 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=