题目内容
已知Sn为数列{an}的前n项和,且对任意n∈N+有Sn=2an-2.
(1)求数列{an}的通项公式;
(2)若不等式a2n-k•an+64≥0对任意n∈N+恒成立,求实数k的取值范围.
(1)求数列{an}的通项公式;
(2)若不等式a2n-k•an+64≥0对任意n∈N+恒成立,求实数k的取值范围.
考点:等比数列的通项公式,数列的函数特性,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)将n用n-1代替得Sn-1=2an-1-2,两式相减得,an=2an-2an-1即2an-1=an,n≥2,利用等比数列的通项公式得到结果;
(2)将(1)中的通项代入不等式a2n-k•an+64≥0得到不等式2n+
≥k恒成立,只需(2n+
)min≥k,利用基本不等式求出最小值得到k的范围.
(2)将(1)中的通项代入不等式a2n-k•an+64≥0得到不等式2n+
| 64 |
| 2n |
| 64 |
| 2n |
解答:
解:(1)∵Sn=2an-2,
∴Sn-1=2an-1-2,
两式相减得,an=2an-2an-1
即2an-1=an,n≥2,
所以{an}为等比数列,a1=2a1-2⇒a1=2,
所以an=2n;…(5分)
(2)a2n-k•an+64≥0⇒22n-k•2n+64≥0⇒22n+64≥k•2n⇒2n+
≥k
…(8分)
只需(2n+
)min≥k,
∵2n+
≥2
=16,当且仅当n=3时取等号.…(11分)
所以16≥k.…(12分)
∴Sn-1=2an-1-2,
两式相减得,an=2an-2an-1
即2an-1=an,n≥2,
所以{an}为等比数列,a1=2a1-2⇒a1=2,
所以an=2n;…(5分)
(2)a2n-k•an+64≥0⇒22n-k•2n+64≥0⇒22n+64≥k•2n⇒2n+
| 64 |
| 2n |
…(8分)
只需(2n+
| 64 |
| 2n |
∵2n+
| 64 |
| 2n |
2n•
|
所以16≥k.…(12分)
点评:本题考查了数列通项的求法;不等式恒成立转化为求最值;利用基本不等式求函数的最值.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
不等式a>b与
>
与同时成立的充要条件为( )
| 1 |
| a |
| 1 |
| b |
| A、a>b>0 | ||||
| B、a>0>b | ||||
C、
| ||||
D、
|
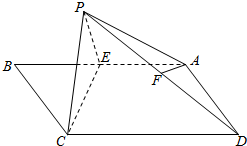 如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.
如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.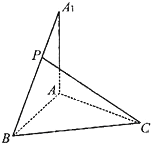 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.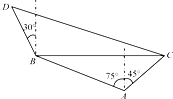 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(