题目内容
已知a，x∈R，a≤x4-4x3+4x2+1恒成立，则a的最大值为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：令y=x4-4x3+4x2+1，对y求导，并求y'=0的解，得到0，1，2三个极值点．其中0，2为极小值点，1为极大值点，所以可知y的最小值，出现在x=0和2处，有y（0）=y（2）=1，所以当a小于等于1时，条件中的式子恒成立，即a的最大值为1．
解答：
解：设y=x4-4x3+4x2+1，
则y′=4x3-12x2+8x，
由y′=0，得x1=0，x2=1，x3=2，
x∈（-∞，0）时，y′＜0；x∈（0，1）时，y′＞0；
x∈（1，2）时，y′0．
∴x=0，x=2时函数有极小值，x=1时函数极大值，
∴y的最小值，出现在x=0和2处，
∵y（0）=y（2）=1，a≤x4-4x3+4x2+1恒成立，
∴a≤1，∴a的最大值为1．
故选：B．
则y′=4x3-12x2+8x，
由y′=0，得x1=0，x2=1，x3=2，
x∈（-∞，0）时，y′＜0；x∈（0，1）时，y′＞0；
x∈（1，2）时，y′0．
∴x=0，x=2时函数有极小值，x=1时函数极大值，
∴y的最小值，出现在x=0和2处，
∵y（0）=y（2）=1，a≤x4-4x3+4x2+1恒成立，
∴a≤1，∴a的最大值为1．
故选：B．
点评：本题考查不等式恒成立时，实数的最大值的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
在△ABC中，sinA≥sinB，则（ ）
| A、a＞b | B、a＜b |
| C、a≥b | D、a≤b |
下列命题，正确的是（ ）
| A、a，b，c∈R，且a＞b，则ac＞bc | ||||
B、a，b∈R，且ab≠0，则
| ||||
| C、复数Z=i-1对应的点在第四象限 | ||||
| D、a，b∈R，且|a|＞|b|，则a2＞b2 |
已知△ABC中，角A、B、C所对的边分别是a、b、c；且a=1，b=2，C=150°，则△ABC的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
不等式a＞b与
＞
与同时成立的充要条件为（ ）
| 1 |
| a |
| 1 |
| b |
| A、a＞b＞0 | ||||
| B、a＞0＞b | ||||
C、
| ||||
D、
|
已知等差数列{an}中，a3+a8=22，a6=7，则a5的值为（ ）
| A、5 | B、15 | C、20 | D、25 |
设a＞0，b＞0，则“a2+b2≤1”是“a+b≤ab+1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
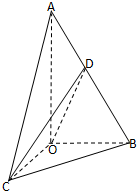如图，在三棱锥A-BOC中，∠OAB=30°，AO⊥平面BOC，AB=4，∠BOC=90°，BO=CO，D是AB的中点．
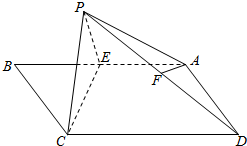如图，在矩形ABCD中，AB=2，BC=1，E为AB的中点，以直线CE为折线将点B折起至点P，并保持∠PEB为锐角，连接PA，PC，PD，取PD的中点F．