题目内容
13.己知等差数列{an}中,a2=2,a5=5.(Ⅰ)若bn=2${\;}^{{a}_{n}}$,求数列{bn}的前n项的和Sn
(Ⅱ)若c1=a1,cn-cn-1=an,求数列{cn}的通项公式.
分析 (Ⅰ)通过a2=2、a5=5可知等差数列{an}的公差d=1,进而可得其通项公式,计算即得结论;
(II)通过(I)可知,当n≥2时cn=$\frac{n(n+1)}{2}$,进而验证当n=1时成立即可.
解答 解:(Ⅰ)∵a2=2,a5=5,
∴d=$\frac{{a}_{5}-{a}_{2}}{3-2}$=1,
所以an=2+(n-2)=n,bn=${2}^{{a}_{n}}$=2n,
于是Sn=21+22+…+2n
=$\frac{2(1-{2}^{n})}{1-2}$
=2n+1-2;
(II)由(I)可知,当n≥2时cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1
=an+an-1+…+a2+a1
=$\frac{n(n+1)}{2}$,
又∵c1=1满足上式,
∴cn=$\frac{n(n+1)}{2}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
4.函数y=$\sqrt{lo{g}_{2}(2x-1)}$的定义域是( )
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,+∞) | D. | [1,+∞) |
1.甲、乙两个粮库要项A,B量诊运送大米,已知甲库将调出100吨大米,乙库将调出80吨大米,A镇至少需要60吨大米,B镇至少需要100吨大米,且甲往B镇运送大米的吨数不少于乙往A镇运送大米的吨数的2倍,两库到两镇运费如表(其中a为常数,$\frac{1}{2}$<a<2).
为了满足上述要求,同时使总运费最省,试问甲、乙粮库应运往A镇各多少吨大米?
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
8.关于x的方程x2-(2a+l)x+a2=0有实数根的一个充分不必要条件是( )
| A. | a>1 | B. | a>-2 | C. | a≥-$\frac{1}{4}$ | D. | a≥-4 |
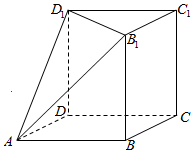 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分