题目内容
8．关于x的方程x2-（2a+l）x+a2=0有实数根的一个充分不必要条件是（ ）| A． | a＞1 | B． | a＞-2 | C． | a≥-$\frac{1}{4}$ | D． | a≥-4 |
分析 关于x的方程x2-（2a+l）x+a2=0有实数根?△≥0，解得a即可判断出．
解答 解：关于x的方程x2-（2a+l）x+a2=0有实数根?△=（2a+1）2-4a2≥0，解得a$≥-\frac{1}{4}$．
∴关于x的方程x2-（2a+l）x+a2=0有实数根的一个充分不必要条件是a＞1．
故选：A．
点评 本题考查了一元二次方程有实数根的充要条件，考查了推理能力与计算能力，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18．已知△ABC内角A，B，C的对边分别为a，b，c，B=60°，b2=ac，则A=（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
19．
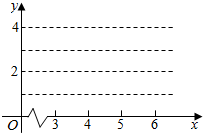某厂通过技术改造降低了产品A对重要原材料G的消耗，如表提供了该厂技术改造后生产产品A的过程记录的产量x（吨）与原材料G相应的消耗量y（吨）的几组对照数据：
（1）请在图a中画出如表数据的散点图；
（2）请根据如表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试根据（2）求出的线性回归方程，预测生产50吨产品A需要消耗原材料G多少吨？参考公式：最小二乘法求线性回归方程
系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
某厂通过技术改造降低了产品A对重要原材料G的消耗，如表提供了该厂技术改造后生产产品A的过程记录的产量x（吨）与原材料G相应的消耗量y（吨）的几组对照数据：| x | 3 | 4 | 5 | 6 |
| y | 1.6 | 2.2 | 3.0 | 3.4 |
（2）请根据如表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试根据（2）求出的线性回归方程，预测生产50吨产品A需要消耗原材料G多少吨？参考公式：最小二乘法求线性回归方程
系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
16．命题p“若sinα=$\frac{1}{2}$，则α=30°；命题q：若点（m，n）在直线x+y+1=0的上方，则m+n+1＞0，下列命题是真命题的是（ ）
| A． | p∨￢q | B． | ￢p∧q | C． | ￢q∧￢q | D． | p∧q |
13．己知等差数列{an}中，a2=2，a5=5．
（Ⅰ）若bn=2${\;}^{{a}_{n}}$，求数列{bn}的前n项的和Sn
（Ⅱ）若c1=a1，cn-cn-1=an，求数列{cn}的通项公式．
（Ⅰ）若bn=2${\;}^{{a}_{n}}$，求数列{bn}的前n项的和Sn
（Ⅱ）若c1=a1，cn-cn-1=an，求数列{cn}的通项公式．
20．已知数列{an}的通项公式是an=（-1）n•（3n+1），则a1+a2+…a100=（ ）
| A． | -300 | B． | -150 | C． | 150 | D． | 300 |
18．已知集合A={x|2x-1＞1}，集合B={x|log3x＜1}，则（∁RA）∩B=（ ）
| A． | （-∞，1] | B． | （-∞，1） | C． | （0，1] | D． | （0，1） |