题目内容
已知函数f(x)=
ex,a,b∈R,且a>0
(1)若函数f(x)在x=-1处取得极值
,试求函数f(x)的解析式及单调区间;
(2)设g(x)=a(x-1)ex-f(x),g′(x)为g(x)的导函数,若存在x0∈(1,+∞),使g(x0)+g′(x0)=0成立,求
的取值范围.
| ax+b |
| x |
(1)若函数f(x)在x=-1处取得极值
| 1 |
| e |
(2)设g(x)=a(x-1)ex-f(x),g′(x)为g(x)的导函数,若存在x0∈(1,+∞),使g(x0)+g′(x0)=0成立,求
| b |
| a |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)先求导函数,再由函数f(x)在x=-1处取得极值
,得
,代入求解参数a,b,然后利用令f′(x)≥0和f′(x)<0求解函数的单调区间;
(2)将f(x)代入g(x)化简,再求g′(x),然后得g(x0)+g′(x0),令其为0,得
=
,令h(x)=
,则问题转化为求h(x)在区间(1,+∞)上的值域,利用导数求解.
| 1 |
| e |
|
(2)将f(x)代入g(x)化简,再求g′(x),然后得g(x0)+g′(x0),令其为0,得
| b |
| a |
| (2x-3)x2 |
| 2x-1 |
| (2x-3)x2 |
| 2x-1 |
解答:
解;(1)由题意f(x)=
ex=(a+
)ex,
∴f′(x)=[(a+
)ex]′═(a+
)′ex+(a+
)(ex)′=(-
+
+a)ex,
由函数f(x)在x=-1处取得极值
,得
,即
,解得
,
则函数f(x)的解析式为f(x)=
ex,定义域为{x|x≠0},
f′(x)=(-
+
+2)ex=-(
-2)(
+1)ex,
又ex>0对x∈R恒成立,
令f′(x)≥0则有-
+
+2≥0,解得-1≤
≤2,且
≠0,即x≤-1或x≥
;
同理令f′(x)<0可解得-1<x<0或0<x<
;
综上,函数f(x)的单调增区间为(-∞,-1]和[
,+∞),单调减区间为(-1,0)和(0,
).
(2)由题意g(x)=a(x-1)ex-f(x)=a(x-1)ex-
ex=axex-2aex-b
,
则g′(x)=axex-aex-b
,
∴g(x)+g′(x)=2axex-3aex-b
=ex(2ax-3a-b
),
由条件存在x0∈(1,+∞),使g(x0)+g′(x0)=0成立得2axex-3aex-b
=0,对x∈(1,+∞)恒成立,
又∵ex>0
∴2ax-3a-b
=0对x∈(1,+∞)恒成立,
化简得
=
,令h(x)=
,则问题转化为求h(x)在区间(1,+∞)上的值域,
求导得h′(x)=
,
令y=4x2-6x+3,为二次函数,图象开口向上,△=-12<0,则4x2-6x+3>0,又x>0,
则h′(x)>0,h(x)在区间(1,+∞)上单调递增,值域为(1,+∞),
所以
的取值范围是(1,+∞).
| ax+b |
| x |
| b |
| x |
∴f′(x)=[(a+
| b |
| x |
| b |
| x |
| b |
| x |
| b |
| x2 |
| b |
| x |
由函数f(x)在x=-1处取得极值
| 1 |
| e |
|
|
|
则函数f(x)的解析式为f(x)=
| 2x+1 |
| x |
f′(x)=(-
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
又ex>0对x∈R恒成立,
令f′(x)≥0则有-
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
同理令f′(x)<0可解得-1<x<0或0<x<
| 1 |
| 2 |
综上,函数f(x)的单调增区间为(-∞,-1]和[
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意g(x)=a(x-1)ex-f(x)=a(x-1)ex-
| ax+b |
| x |
| ex |
| x |
则g′(x)=axex-aex-b
| xex-ex |
| x2 |
∴g(x)+g′(x)=2axex-3aex-b
| 2xex-ex |
| x2 |
| 2x-1 |
| x2 |
由条件存在x0∈(1,+∞),使g(x0)+g′(x0)=0成立得2axex-3aex-b
| 2xex-ex |
| x2 |
又∵ex>0
∴2ax-3a-b
| 2x-1 |
| x2 |
化简得
| b |
| a |
| (2x-3)x2 |
| 2x-1 |
| (2x-3)x2 |
| 2x-1 |
求导得h′(x)=
| 2x(4x2-6x+3) |
| (2x+1)2 |
令y=4x2-6x+3,为二次函数,图象开口向上,△=-12<0,则4x2-6x+3>0,又x>0,
则h′(x)>0,h(x)在区间(1,+∞)上单调递增,值域为(1,+∞),
所以
| b |
| a |
点评:本题考查了导数在函数的单调性和最值求解中的综合应用,属于比较复杂的问题,注意利用转化的思想求解问题.

练习册系列答案
相关题目
已知三棱锥O-ABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O-ABC的体积为
,则球O的表面积是( )
| ||
| 4 |
| A、544π | ||
| B、16π | ||
C、
| ||
| D、64π |
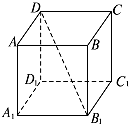
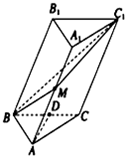 如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.