题目内容
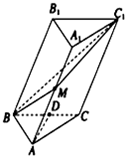 如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.(1)若D是BC的中点.求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)若截面MBC1⊥侧面BB1C1C..求证:AM=MA1.
考点:平面与平面垂直的判定,空间中直线与直线之间的位置关系
专题:证明题,空间位置关系与距离
分析:(1)先证明平面ABC⊥平面BB1C1C,可知AD⊥平面BB1C1C,从而可证AD⊥CC1;
(2)取BC1的中点E,连接DE、ME,先证明MA
ED,从而有EM∥AD,由(1)知AD⊥平面BB1C1C.即可证明平面BMC1⊥平面BB1C1C.
(3)在图中,过M作ME⊥BC1于E,由截面MBC1⊥侧面BB1C1C,可证四边形MADE为平行四边形,有AM=DE,可证DE∥CC1,即可证明AM=MA1.
(2)取BC1的中点E,连接DE、ME,先证明MA
| ∥ |
. |
(3)在图中,过M作ME⊥BC1于E,由截面MBC1⊥侧面BB1C1C,可证四边形MADE为平行四边形,有AM=DE,可证DE∥CC1,即可证明AM=MA1.
解答:
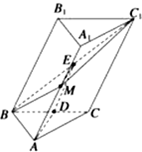 证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC.
证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC.
∵平面ABC⊥平面BB1C1C,交线为BC.
∴由面面垂直的性质定理,
可知AD⊥平面BB1C1C.
又平面CC1?BB1C1C,
∴AD⊥CC1.----------------(4分)
(2)取BC1的中点E,连接DE、ME.在△BCC1中,D、E分别是BC、BC1的中点,
∵M是AA1的中点(由AM=MA1知)
∴MA
ED,∴EM∥AD,
由(1)知AD⊥平面BB1C1C.
∴ME⊥平面BB1C1C.
∴平面BMC1⊥平面BB1C1C.-------------(9分)
(3)在图中,过M作ME⊥BC1于E,
∵截面MBC1⊥侧面BB1C1C,
∴ME⊥侧面BB1C1C
又AD⊥侧面BB1C1C,
∴ME∥AD,又AM∥侧面BB1C1C,平面AMED∩侧面BB1C1C=DE,
∴AM∥DE,
∴四边形MADE为平行四边形,
∴AM=DE,
∵CC1∥AM,
∴DE∥CC1,又D为BC中点,
∴E为BC1中点,
∴AM=DE=
CC1
∴AM=MA1.---------------(14分)
 证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC.
证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC.∵平面ABC⊥平面BB1C1C,交线为BC.
∴由面面垂直的性质定理,
可知AD⊥平面BB1C1C.
又平面CC1?BB1C1C,
∴AD⊥CC1.----------------(4分)
(2)取BC1的中点E,连接DE、ME.在△BCC1中,D、E分别是BC、BC1的中点,
∵M是AA1的中点(由AM=MA1知)
∴MA
| ∥ |
. |
由(1)知AD⊥平面BB1C1C.
∴ME⊥平面BB1C1C.
∴平面BMC1⊥平面BB1C1C.-------------(9分)
(3)在图中,过M作ME⊥BC1于E,
∵截面MBC1⊥侧面BB1C1C,
∴ME⊥侧面BB1C1C
又AD⊥侧面BB1C1C,
∴ME∥AD,又AM∥侧面BB1C1C,平面AMED∩侧面BB1C1C=DE,
∴AM∥DE,
∴四边形MADE为平行四边形,
∴AM=DE,
∵CC1∥AM,
∴DE∥CC1,又D为BC中点,
∴E为BC1中点,
∴AM=DE=
| 1 |
| 2 |
∴AM=MA1.---------------(14分)
点评:本题主要考察了平面与平面垂直的判定,空间中直线与直线之间的位置关系,恰当的添加辅助线是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
已知幂函数f(x)=kxα(k∈R,α∈R)的图象过点(
,
),则k+α=( )
| 1 |
| 2 |
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
设Sn是等差数列{an}的前n项和,若
=
,则
=( )
| a5 |
| a3 |
| 5 |
| 9 |
| S9 |
| S5 |
| A、1 | ||
| B、-1 | ||
| C、2 | ||
D、
|