题目内容
已知三棱锥O-ABC，A，B，C三点均在球心为O的球表面上，AB=BC=1，∠ABC=120°，三棱锥O-ABC的体积为
，则球O的表面积是（ ）
| ||
| 4 |
| A、544π | ||
| B、16π | ||
C、
| ||
| D、64π |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：求出底面三角形的面积，利用三棱锥的体积求出O到底面的距离，求出底面三角形的所在平面圆的半径，通过勾股定理求出球的半径，即可求解球的体积．
解答：
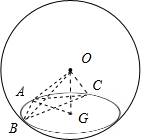解：三棱锥O-ABC，A、B、C三点均在球心O的表面上，且AB=BC=1，∠ABC=120°，BC=
，
∴S△ABC=
×1×1×sin120°=
，
∵三棱锥O-ABC的体积为
，
△ABC的外接圆的圆心为G，
∴OG⊥⊙G，
外接圆的半径为：GA=
=1，
∴
S△ABC•OG=
，即
×
OG=
，
OG=
，
球的半径为：
=4．
球的表面积：4π42=64π．
故选：D
解：三棱锥O-ABC，A、B、C三点均在球心O的表面上，且AB=BC=1，∠ABC=120°，BC=| 3 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
∵三棱锥O-ABC的体积为
| ||
| 4 |
△ABC的外接圆的圆心为G，
∴OG⊥⊙G，
外接圆的半径为：GA=
| ||
| 2sin120° |
∴
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 4 |
OG=
| 15 |
球的半径为：
| AG2+OG2 |
球的表面积：4π42=64π．
故选：D
点评：本题考查球的表面积的求法，球的内含体与三棱锥的关系，考查空间想象能力以及计算能力．
练习册系列答案
名校课堂系列答案
相关题目
小李从甲地到乙地的平均速度为a，从乙地到甲地的平均速度为b（a＞b＞0），他往返甲乙两地的平均速度为v，则（ ）
A、v=
| ||||
B、v=
| ||||
C、
| ||||
D、b＜v＜
|
函数f（x）=
的图象大致为（ ）
|
A、 |
B、 |
C、 |
D、 |