题目内容
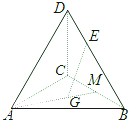 如图,四面体ABCD中,G为△ABC的重心,
如图,四面体ABCD中,G为△ABC的重心,| BE |
| ED |
| AB |
| AC |
| AD |
| GE |
考点:空间向量的基本定理及其意义
专题:空间向量及应用
分析:利用向量的三角形法则、共线定理及其平行四边形法则即可得出.
解答:
解:∵
=
+
,
=
,
=
(
+
),
=
+
,
=
,
=
-
,
=
,
=
-
.
∴
=
×
(
+
)+
(
-
)+
(
-
)=-
+
.
故答案为:-
+
.
| GE |
| GM |
| ME |
| GM |
| 1 |
| 3 |
| AM |
| AM |
| 1 |
| 2 |
| AB |
| AC |
| ME |
| MB |
| BE |
| MB |
| 1 |
| 2 |
| CB |
| CB |
| AB |
| AC |
| BE |
| 2 |
| 3 |
| BD |
| BD |
| AD |
| AB |
∴
| GE |
| 1 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| 2 |
| 3 |
| AD |
| AB |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AD |
故答案为:-
| 1 |
| 3 |
. |
| AC |
| 2 |
| 3 |
| AD |
点评:本题考查了向量的三角形法则、共线定理及其平行四边形法则,属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
一个算法的程序框图如图,则其输出结果是( )


| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
已知集合M={x|-1<x<1},N={x|3x>1},则M∩N=( )
| A、∅ |
| B、{x|x>0} |
| C、{x|x<1} |
| D、{x|0<x<1} |
执行如图所示的程序框图,输出的M的值是( )


| A、2 | ||
| B、-1 | ||
C、
| ||
| D、-2 |
 某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为
某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为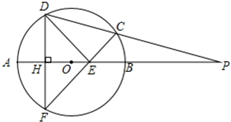 如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.
如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.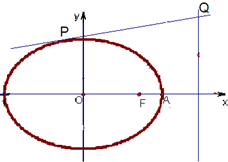 已知椭圆C:
已知椭圆C: