题目内容
一个算法的程序框图如图,则其输出结果是( )


| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:程序框图
专题:算法和程序框图
分析:程序运行的功能是求S=sin
+sin
+sin
+…+sin
的值,利用三角函数的周期性与诱导公式求得S的值.
| π |
| 4 |
| 2π |
| 4 |
| 3π |
| 4 |
| 2014π |
| 4 |
解答:
解:由程序框图知:程序运行的功能是求S=sin
+sin
+sin
+…+sin
的值,
∵sin
+sin
+sin
+sin
+sin
+sin
+sin
+sin
=sin
+sin
+sin
+sin
-sin
-sin
-sin
-sin
=0,
2014=8×251+6,
∴S=251×0+sin
+sin
+sin
+sin
+sin
+sin
=
.
故选:B.
| π |
| 4 |
| 2π |
| 4 |
| 3π |
| 4 |
| 2014π |
| 4 |
∵sin
| nπ |
| 4 |
| (n+1)π |
| 4 |
| (n+2)π |
| 4 |
| (n+3)π |
| 4 |
| (n+4)π |
| 4 |
| (n+5)π |
| 4 |
| (n+6)π |
| 4 |
| (n+7)π |
| 4 |
=sin
| nπ |
| 4 |
| (n+1)π |
| 4 |
| (n+2)π |
| 4 |
| (n+3)π |
| 4 |
| nπ |
| 4 |
| (n+1)π |
| 4 |
| (n+2)π |
| 4 |
| (n+3)π |
| 4 |
2014=8×251+6,
∴S=251×0+sin
| π |
| 4 |
| 2π |
| 4 |
| 3π |
| 4 |
| 4π |
| 4 |
| 5π |
| 4 |
| 6π |
| 4 |
| ||
| 2 |
故选:B.
点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答此类问题的关键.

练习册系列答案
相关题目
某程序框图如图所示,该程序运行后输出的S的值是( )


| A、-2 | ||
B、
| ||
| C、3 | ||
D、-
|
若函数f(x)=4x2-kx+2k在[-1,2]上为减函数,则实数k的取值范围为( )
| A、[16,+∞) |
| B、(-∞,-8] |
| C、[-8,16] |
| D、(-∞,-8]∩[16,+∞) |
设球的半径为R,P、Q是球面上北纬60°圈上的两点,这两点在纬度圈上的劣弧的长是
,则这两点的球面距离是( )
| πR |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
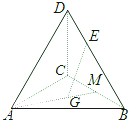 如图,四面体ABCD中,G为△ABC的重心,
如图,四面体ABCD中,G为△ABC的重心,