题目内容
12.若动圆C过定点A(4,0),且在y轴上截得弦MN的长为8,则动圆圆心C的轨迹方程是( )| A. | x2=8y | B. | x2=8y(x≠0) | C. | y2=8x | D. | y2=8x(x≠0) |
分析 设圆心C(x,y),过点C作CE⊥y 轴,垂足为E,利用垂径定理可得|ME|=4,又|CA|2=|CM|2=|ME|2+|EC|2,利用两点间的距离公式即可得出.
解答 解:设圆心C(x,y),过点C作CE⊥y 轴,垂足为E,则|ME|=4,
∴|CA|2=|CM|2=|ME|2+|EC|2,
∴(x-4)2+y2=42+x2,化为y2=8x.
故选:C.
点评 本题综合考查了抛物线的标准方程及其性质、垂径定理、两点间的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
2.已知偶函数f(x)在[0,+∞)上是增函数,且f(2)=0,则不等式f(x+1)<0的解集是( )
| A. | [0,2) | B. | (-2,2) | C. | (-1,3) | D. | (-3,1) |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\sqrt{2}$,则其渐近线方程为( )
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{{\sqrt{2}}}{2}x$ | D. | $y=±\frac{1}{2}x$ |
20.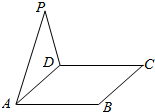 如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
 如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )| A. | 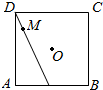 | B. | 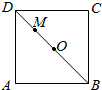 | C. |  | D. | 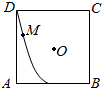 |
7.垂直于直线x-2y+2=0且与圆x2+y2=5相切的直线的方程是( )
| A. | 2x+y+5=0或2x+y-5=0 | B. | $2x+y+\sqrt{5}=0$或$2x+y-\sqrt{5}=0$ | ||
| C. | 2x-y+5=0或2x-y-5=0 | D. | $2x-y+\sqrt{5}=0$或$2x-y-\sqrt{5}=0$ |
2.给出的四个命题,其中正确的是( )
| A. | ?x0∈R,x${\;}_{0}^{2}$+2x0+2=0 | B. | ?x∈N,x3>c2 | ||
| C. | 若x>1,则x2>1 | D. | 若a>b,则a2>b2 |
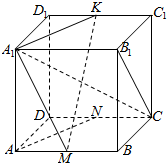 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证: