题目内容
17.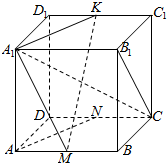 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:(1)AN∥平面A1MK;
(2)MK⊥平面A1B1C.
分析 (1),要证明AN∥平面A1MK,只需证明AN平行于平面A1MK内的一条直线,容易证明AN∥A1K,从而得证;
(2),要证明平面A1B1C⊥MK,只需证明BC1⊥平面A1B1C,BC1∥MK即可,从而问题得以解决.
解答 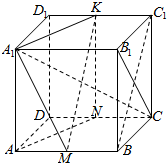 证明:(1)连接KN,由于K、N为CD,C1D1的中点,
证明:(1)连接KN,由于K、N为CD,C1D1的中点,
所以KN平行且等于AA1,
AA1KN为平行四边形⇒AN∥A1K,
而A1K?平面A1MK,AN?平面A1MK,
从而AN∥平面A1MK.
(2)连接BC1,由于M、K为AB、C1D1的中点,
所以:KC1与MB平行且相等,
从而:KC1MB为平行四边形,
所以:MK∥BC1,
而:BC1⊥B1C,BC1⊥A1B1,
从而:BC1⊥平面A1B1C,
所以:MK⊥平面A1B1C.
点评 本题考查线面平行的判定定理、面面垂直的判定定理的使用,要注意其中的转化思想的应用,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
8.设f(x)是定义在R上的增函数,且对任意x,都有f(-x)+f(x)=0恒成立,如果实数m,n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是( )
| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
5.g(x)的定义域为R,且满足g(x)+xg′(x)-g′(x)<0,则y=g(x)的零点个数为( )
| A. | 1 | B. | 0 | C. | 2 | D. | 0或2 |
12.若动圆C过定点A(4,0),且在y轴上截得弦MN的长为8,则动圆圆心C的轨迹方程是( )
| A. | x2=8y | B. | x2=8y(x≠0) | C. | y2=8x | D. | y2=8x(x≠0) |
9.以下有关命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | |
| D. | 对于命题p:?x∈R,使得x2+x-1<0,则¬p:?x∈R,则x2+x+1≥0 |