题目内容
4.已知函数f(x)=loga(2+x)-loga(2-x)(0<a<1).(1)判断f(x)的奇偶性;
(2)解不等式f(x)≥loga(3x).
分析 (1)根据已知中函数的解析式,结合函数奇偶性的概念判断即可;
(2)根据函数的单调性,将不等式f(x)≥loga(3x)化为:0<$\frac{2+x}{2-x}$≤3x,解得答案;
解答 解:(1)由$\left\{\begin{array}{l}2+x>0\\ 2-x>0\end{array}\right.$得:x∈(-2,2),
即函数的定义域(-2,2)关于原点对称,
又由f(-x)=loga(2-x)-loga(2+x)=-[loga(2+x)-loga(2-x)]=-f(x),
故函数f(x)为奇函数;
(2)∵0<a<1,
∴y=loga(2+x)为减函数,y=loga(2-x)为增函数,
故函数f(x)=loga(2+x)-loga(2-x)(0<a<1)为减函数,
则不等式f(x)≥loga(3x)可化为:0<$\frac{2+x}{2-x}$≤3x,
解得:x∈[$\frac{2}{3}$,1].
点评 本题考查的知识点是函数的奇偶性,函数的单调性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
12.若动圆C过定点A(4,0),且在y轴上截得弦MN的长为8,则动圆圆心C的轨迹方程是( )
| A. | x2=8y | B. | x2=8y(x≠0) | C. | y2=8x | D. | y2=8x(x≠0) |
19.直线5x-12y+8=0与圆x2+y2-2x=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 无法判断 |
9.以下有关命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | |
| D. | 对于命题p:?x∈R,使得x2+x-1<0,则¬p:?x∈R,则x2+x+1≥0 |
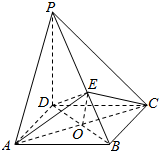 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$.O为AC与BD的交点,E为棱PB上一点
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$.O为AC与BD的交点,E为棱PB上一点