题目内容
已知四棱锥底面四边形中顺次三个内角的大小之比为2:3:4,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( )
A、
| ||
| B、60° | ||
C、
| ||
| D、无法确定的 |
考点:直线与平面所成的角
专题:空间位置关系与距离
分析:因为棱锥的各侧棱与底面所成角相等,所以顶点在底面内的射影是底面四边形的外接圆圆心,底面四边形ABCD是圆内接四边形.由此能求出底面四边形的最小角.
解答:
解:因为棱锥的各侧棱与底面所成角相等,
所以顶点在底面内的射影是底面四边形的外接圆圆心,
底面四边形ABCD是圆内接四边形.
设A:B:C=2:3:4,
由于A+C=180°,
因此A=60°,C=120°,B=D=90°,
故最小角为A=60°.
故选:B.
所以顶点在底面内的射影是底面四边形的外接圆圆心,
底面四边形ABCD是圆内接四边形.
设A:B:C=2:3:4,
由于A+C=180°,
因此A=60°,C=120°,B=D=90°,
故最小角为A=60°.
故选:B.
点评:本题考查底面四边形的最小角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在正方体ABCD-A1B1C1D1中,与棱AA1垂直的棱共有( )条.
| A、2 | B、4 | C、6 | D、8 |
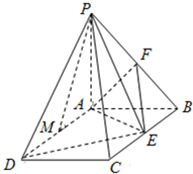 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=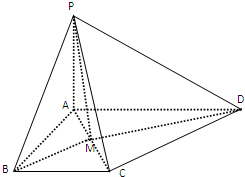 如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.
如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.