题目内容
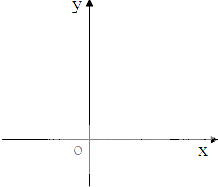
已知函数y=x2-4x+6①当x∈R时，画出函数图象，根据图象写出函数的增区间、减区间；
②当x∈[1，4]时，求出函数的最大值、最小值．
考点：二次函数的性质,函数的图象
专题：函数的性质及应用
分析：①由函数的解析式画出它的图象，如图．
②结合图形，利用二次函数的性质求得，当x∈[1，4]时，函数的最小值和最大值．
②结合图形，利用二次函数的性质求得，当x∈[1，4]时，函数的最小值和最大值．
解答：
解：①∵函数y=x2-4x+6=（x-2）2+2，对称轴为x=2，
可得它的图象，如图．
②结合图形可得，当x∈[1，4]时，
则x=2时，函数取得最小值为2，
x=4时，函数取得最大值为6．
解：①∵函数y=x2-4x+6=（x-2）2+2，对称轴为x=2，可得它的图象，如图．
②结合图形可得，当x∈[1，4]时，
则x=2时，函数取得最小值为2，
x=4时，函数取得最大值为6．
点评：本题主要考查二次函数的图象和性质，体现了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
利用数学归纳法证明不等式1+
+
+…+
＜n（n≥2，n∈N）的过程中，进行第一步验证时，不等式左边应为（ ）之和．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A、1项 | B、2项 | C、3项 | D、4项 |
若6名学生排成一列，则学生甲、乙、丙三人互不相邻的排位方法种数为（ ）
| A、24 | B、36 | C、72 | D、144 |
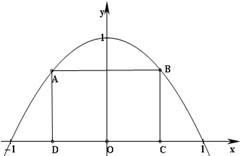如图所示，抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在x轴上．已知工业用地每单位面积价值为3a元（a＞0），其它的三个边角地块每单位面积价值a元．
如图，在四棱锥P-ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：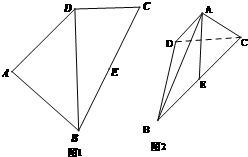
如图，四边形ABCD中（图1），E是BC的中点，DB=2，DC=1，BC=