题目内容
如图，在四棱锥P-ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：（1）PA∥平面MDB；
（2）PD⊥BC．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连接AC，交BD与点O，连接OM，先证明出MO∥PA，进而根据线面平行的判定定理证明出PA∥平面MDB．
（2）先证明出BC⊥平面PCD，进而根据线面垂直的性质证明出BC⊥PD．
（2）先证明出BC⊥平面PCD，进而根据线面垂直的性质证明出BC⊥PD．
解答：
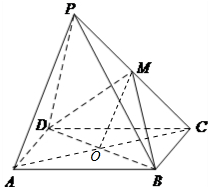证明：（1）连接AC，交BD与点O，连接OM，
∵M为PC的中点，O为AC的中点，
∴MO∥PA，
∵MO?平面MDB，PA?平面MDB，
∴PA∥平面MDB．
（2）∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，BC?平面ABCD，BC⊥CD，
∴BC⊥平面PCD，
∵PD?平面PCD，
∴BC⊥PD．
证明：（1）连接AC，交BD与点O，连接OM，∵M为PC的中点，O为AC的中点，
∴MO∥PA，
∵MO?平面MDB，PA?平面MDB，
∴PA∥平面MDB．
（2）∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，BC?平面ABCD，BC⊥CD，
∴BC⊥平面PCD，
∵PD?平面PCD，
∴BC⊥PD．
点评：本题主要考查了线面平行的判定和线面垂直的判定．判定的关键是先找到到线线平行，线线垂直．
练习册系列答案
相关题目
同时掷两个骰子，“向上的点数之和大于8”的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，四棱锥P-ABCD中，PA⊥面ABCD，E、F分别为BD、PD的中点，EA=EB．
已知函数y=x2-4x+6