题目内容
若6名学生排成一列，则学生甲、乙、丙三人互不相邻的排位方法种数为（ ）
| A、24 | B、36 | C、72 | D、144 |
考点：计数原理的应用
专题：排列组合
分析：不相邻的问题，采用插空法，先排除学生甲、乙、丙三人的另外三个人形成4个空，然后插入甲、乙、丙三人，问题得以解决．
解答：
解：先排除学生甲、乙、丙三人的另外三个人形成4个空，然后插入甲、乙、丙三人种数为
•
=144．
故选：D
| A | 3 3 |
| A | 3 4 |
故选：D
点评：本题考查排列、组合的运用，关键要掌握特殊问题的处理方法，如相邻问题用捆绑法，不相邻问题用插空法，属于中档题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在等比数列{an}中，S7=10，S14=30，求S21=（ ）
| A、40 | B、70 | C、60 | D、80 |
设Sn是等比数列{an}的前n项和，S3，S9，S6成等差数列，且a2+a5=2am，则m等于（ ）
| A、6 | B、7 | C、8 | D、10 |
在复数范围内，方程x2=-3的解是（ ）
A、±
| ||
| B、-3 | ||
C、±
| ||
| D、±3i |
已知函数f（x）=
（sint-lgt）dt（x＞1），则f（x）的极大值点的个数为（ ）
| ∫ | x 1 |
| A、0 | B、1 | C、2 | D、3 |
已知函数y=x2-4x+6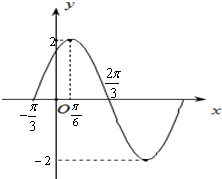
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示．