题目内容
若方程|ax|=x+a(a>0)有两个解,则a的取值范围是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:讨论x的符号,利用分段函数的图象和性质,即可得到结论.
解答:
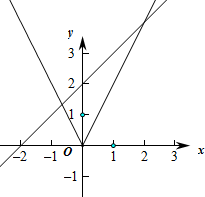 解:作出函数f(x)=|ax|=
解:作出函数f(x)=|ax|=
和g(x)=x+a的图象如图:
则当x<0时,∵a>0,∴此时方程程|ax|=x+a(a>0)一定有一个负根,
要使方程|ax|=x+a(a>0)有两个解,则等价为当x>0时,方程有一个正根,
即ax=x+a,有一正根,
则(a-1)x=a,则x=
>0,
∵a>0,∴a-1>0,解得a>1,
故a的取值范围是(1,+∞),(如图)
故答案为:(1,+∞)
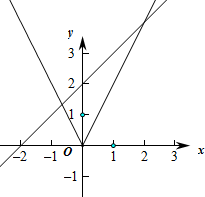 解:作出函数f(x)=|ax|=
解:作出函数f(x)=|ax|=
|
则当x<0时,∵a>0,∴此时方程程|ax|=x+a(a>0)一定有一个负根,
要使方程|ax|=x+a(a>0)有两个解,则等价为当x>0时,方程有一个正根,
即ax=x+a,有一正根,
则(a-1)x=a,则x=
| a |
| a-1 |
∵a>0,∴a-1>0,解得a>1,
故a的取值范围是(1,+∞),(如图)
故答案为:(1,+∞)
点评:本题主要考查方程根的个数的应用,利用分段函数,进行转化是解决本题的关键.本题也可以利用数形结合进行求解.

练习册系列答案
相关题目
已知平面上的非零向量
,
,
满足
+
+
=
,|
|=|
|=1,且cos<
,
>=-
,则△P1P2P3的形状为( )
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| 0 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| 4 |
| 5 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |