题目内容
已知数列{an}的前n项和Sn满足:Sn+an=n(n=1,2,3…).
(1)求a1,并证明:数列{an-1}为等比数列;
(2)设bn=(2-n)(an-1)(n=1,2,3…),如果对任意n∈N*,bn≤t2-
t,求t的范围;
(3)记Cn=-
试问{Cn}中是否存在一项Ck,使得Ck恰好可以表示为该数列中连续P(P∈N,P≥2)项的和?请说明理由.
(1)求a1,并证明:数列{an-1}为等比数列;
(2)设bn=(2-n)(an-1)(n=1,2,3…),如果对任意n∈N*,bn≤t2-
| 1 |
| 4 |
(3)记Cn=-
| 1 |
| an-1 |
考点:等比关系的确定,数列递推式
专题:等差数列与等比数列
分析:(1)利用Sn+an=n,得Sn+1+an+1=n+1,两式相减,整理可得数列{an-1是以-
为首项,以
为公比的等比数列;
(2)先确定bn=(2-n)(an-1)的,通项公式,再利用bn+1-bn,确定bn有最大值b,可求实数t的取值范围.
(3)求出Cn的表达式,利用反证法即可证明结论是否成立.
| 1 |
| 2 |
| 1 |
| 2 |
(2)先确定bn=(2-n)(an-1)的,通项公式,再利用bn+1-bn,确定bn有最大值b,可求实数t的取值范围.
(3)求出Cn的表达式,利用反证法即可证明结论是否成立.
解答:
解:(1)由题可知:Sn+an=n,①
Sn+1+an+1=n+1,②
②-①可得2an+1-an=1
即an+1-1=
(an-1),
又a1-1=-
,
∴数列{an-1是以-
为首项,以
为公比的等比数列.
(2)由(1)可得an=1-(
)n,
∴bn=(2-n)(an-1)=
,
由bn+1-bn=
-
=
>0,可得n<3,
由bn+1-bn<0可得n>3,
即b1<b2<b3=b4,b4>b5>…>bn>…,
故bn有最大值b3=b4=
,
∴对任意n∈N*,都有bn+
t≤t2,等价于对任意n∈N*,都有
≤t2-
t成立,
∴t2-
t-
≥0,
解得t≥
或t≤-
,
∴实数t的取值范围是(-∞,-
]∪[
,+∞);
(3)由(1)得:Cn=-
=2n,
设{Ck}的前n项和为Sn,则Sn=2n+1-1,
假设存在Ck满足(3)中条件,则存在正整数m,使得S(m+P)-Sm=2m+1(2P-1)=2k=Ck成立,
即存在m,使2P-1=2k-m-1成立,
而2P-1为大于3的奇数,2k-m-1只有1和偶数两种情况出现,两者没有交集不可能相等.
∴假设不成立.
∴{Cn}中不存在满足条件(3)的项Ck.
Sn+1+an+1=n+1,②
②-①可得2an+1-an=1
即an+1-1=
| 1 |
| 2 |
又a1-1=-
| 1 |
| 2 |
∴数列{an-1是以-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)可得an=1-(
| 1 |
| 2 |
∴bn=(2-n)(an-1)=
| n-2 |
| 2n |
由bn+1-bn=
| n+1-2 |
| 2n+1 |
| n-2 |
| 2n |
| 3-n |
| 2n+1 |
由bn+1-bn<0可得n>3,
即b1<b2<b3=b4,b4>b5>…>bn>…,
故bn有最大值b3=b4=
| 1 |
| 8 |
∴对任意n∈N*,都有bn+
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
∴t2-
| 1 |
| 4 |
| 1 |
| 8 |
解得t≥
| 1 |
| 2 |
| 1 |
| 4 |
∴实数t的取值范围是(-∞,-
| 1 |
| 4 |
| 1 |
| 2 |
(3)由(1)得:Cn=-
| 1 |
| an-1 |
设{Ck}的前n项和为Sn,则Sn=2n+1-1,
假设存在Ck满足(3)中条件,则存在正整数m,使得S(m+P)-Sm=2m+1(2P-1)=2k=Ck成立,
即存在m,使2P-1=2k-m-1成立,
而2P-1为大于3的奇数,2k-m-1只有1和偶数两种情况出现,两者没有交集不可能相等.
∴假设不成立.
∴{Cn}中不存在满足条件(3)的项Ck.
点评:本题主要考查数列递推式,考查等比数列的证明,考查恒成立问题,确定数列的通项,求出数列的最大值是解题的关键,综合性较强,运算量较大.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.
如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.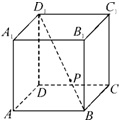 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有