题目内容
函数f(x)=x3-3ax2+3b2x,(a,b∈R)
(Ⅰ)若a=1,b=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)在区域D={(x,y)|(x-1)2+y2≤1,x,y∈R}中随机抽取一点,该点的横、纵坐标分别记为a、b,求函数f(x)在R上是增函数的概率;
(Ⅲ)若0<a<b,不等式f(
)>f(
)对任意的x∈(1,+∞)恒成立,求整数k的最大值.
(Ⅰ)若a=1,b=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)在区域D={(x,y)|(x-1)2+y2≤1,x,y∈R}中随机抽取一点,该点的横、纵坐标分别记为a、b,求函数f(x)在R上是增函数的概率;
(Ⅲ)若0<a<b,不等式f(
| 1+1nx |
| x-1 |
| k |
| x |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)把a=1,b=0代入函数f(x)=x3-3ax2+3b2x中,对其进行求导,求出x=1处的导数,得出直线的斜率,写出曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)基本事件是以A(1,0)为圆心,半径为1的圆及圆的内部,它构成的测度为S=π,所求事件为以A(1,0)为圆心,半径为1的圆及圆的内部,且满足f(x)在R上是增函数,求出其面积,即可求函数f(x)在R上是增函数的概率;
(Ⅲ)对f(x)进行求导,利用导数研究其单调性,可得f(x)是单调递减的,根据不等式,不等式f(
)>f(
)?
>k,对x∈(1,+∞)恒成立,利用常数分离法进行求解.
(Ⅱ)基本事件是以A(1,0)为圆心,半径为1的圆及圆的内部,它构成的测度为S=π,所求事件为以A(1,0)为圆心,半径为1的圆及圆的内部,且满足f(x)在R上是增函数,求出其面积,即可求函数f(x)在R上是增函数的概率;
(Ⅲ)对f(x)进行求导,利用导数研究其单调性,可得f(x)是单调递减的,根据不等式,不等式f(
| 1+1nx |
| x-1 |
| k |
| x |
| (1+lnx)x |
| x-1 |
解答:
解:(Ⅰ)当a=1,b=0时,f(x)=x3-3x2 所以f(1)=-2 即切点为P(1,-2)
因为f′(x)=3x2-6x所以 f′(1)=3-6=-3,
所以切线方程为y+2=-3(x-1)即y=-3x+1,
(Ⅱ)基本事件是以A(1,0)为圆心,半径为1的圆及圆的内部,它构成的测度为S=π.
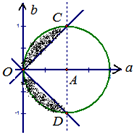
所求事件为以A(1,0)为圆心,半径为1的圆及圆的内部,且满足f(x)在R上是增函数,即f′(x)=3x2-6ax+3b2≥0,∴△≤0,∴|a|≤|b|,是弓形OC与弓形OD及弓形的内部,其测度为2(
-
)=
-1,
∴函数f(x)在R上是增函数的概率为
-
;
(Ⅲ)f′(x)=3x2-6ax+3b2,
由于0<a<b,所以△=36a2-36b2=36(a+b)(a-b)<0,
所以函数f(x)在R上单调递增
所以不等式f(
)>f(
)?
>k,对x∈(1,+∞)恒成立,
构造h(x)=
,h′(x)=
构造g(x)=x-lnx-2,g′(x)=
,
对x∈(1,+∞),g′(x)=
>0
所以g(x)=x-lnx-2在x∈(1,+∞)递增,
g(1)=-1,g(2)=-ln2,g(3)=1-ln3<0,g(4)=2-ln4>0,
所以?x0∈(3,4),g(x2)=x0-lnx0-2=0,
所以x∈(1,x0),g(x)<0,h(x)<0,
所以,所以h(x)=
在(1,x2)递减x∈(x0,+∞),g(x)>0,h(x)>0,
所以h(x)=
在(x0,+∞)递增,所以,h(x)min=h(x0)=
结合g(x0)=x0-lnx0-2=0得到,h(x)min=h(x0)=x0∈(3,4)
所以k<
对x∈(1,+∞)恒成立?k<h(x)min,
所以k≤3,整数k的最大值为3.
因为f′(x)=3x2-6x所以 f′(1)=3-6=-3,
所以切线方程为y+2=-3(x-1)即y=-3x+1,
(Ⅱ)基本事件是以A(1,0)为圆心,半径为1的圆及圆的内部,它构成的测度为S=π.

所求事件为以A(1,0)为圆心,半径为1的圆及圆的内部,且满足f(x)在R上是增函数,即f′(x)=3x2-6ax+3b2≥0,∴△≤0,∴|a|≤|b|,是弓形OC与弓形OD及弓形的内部,其测度为2(
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
∴函数f(x)在R上是增函数的概率为
| 1 |
| 2 |
| 1 |
| π |
(Ⅲ)f′(x)=3x2-6ax+3b2,
由于0<a<b,所以△=36a2-36b2=36(a+b)(a-b)<0,
所以函数f(x)在R上单调递增
所以不等式f(
| 1+1nx |
| x-1 |
| k |
| x |
| (1+lnx)x |
| x-1 |
构造h(x)=
| (1+lnx)x |
| x-1 |
| x-lnx-2 |
| (x-1)2 |
构造g(x)=x-lnx-2,g′(x)=
| x-1 |
| x |
对x∈(1,+∞),g′(x)=
| x-1 |
| x |
所以g(x)=x-lnx-2在x∈(1,+∞)递增,
g(1)=-1,g(2)=-ln2,g(3)=1-ln3<0,g(4)=2-ln4>0,
所以?x0∈(3,4),g(x2)=x0-lnx0-2=0,
所以x∈(1,x0),g(x)<0,h(x)<0,
所以,所以h(x)=
| (1+lnx)x |
| x-1 |
所以h(x)=
| (1+lnx)x |
| x-1 |
| (1+lnx0)x0 |
| x0-1 |
结合g(x0)=x0-lnx0-2=0得到,h(x)min=h(x0)=x0∈(3,4)
所以k<
| (1+lnx)x |
| x-1 |
所以k≤3,整数k的最大值为3.
点评:本题考查函数、导数、概率知识及其应用,考查运算求解能力,考查函数与方程思想、分类与整合思想、数形结合思想及化归与转化思想.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
对于P(K2>k),当k>2.706时,就约有( )的把握认为“x与y有关系”
| A、99% | B、95% |
| C、90% | D、以上都不对 |

 样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的
样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的