题目内容
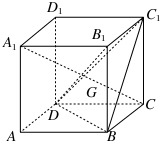如图，在棱长为a的正方体ABCD-A1B1C1D1中，G为△BC1D的重心，（1）试证：A1，G，C三点共线
（2）试证：A1C⊥平面BC1D
（3）求点C到平面BC1D的距离．
考点：点、线、面间的距离计算,直线与平面垂直的判定
专题：综合题,空间位置关系与距离
分析：（1）利用向量法，证明
∥
，利用
与
有公共点C，可得A1、G、C三点共线；
（2）利用向量法，证明CA1⊥BC1，CA1⊥BD，即可证明A1C⊥平面BC1D；
（3）|
|=
a，因此|
|=
a，即可求出点C到平面BC1D的距离．
| CG |
| CA1 |
| CG |
| CA1 |
（2）利用向量法，证明CA1⊥BC1，CA1⊥BD，即可证明A1C⊥平面BC1D；
（3）|
| CA1 |
| 3 |
| CG |
| ||
| 3 |
解答：
（1）证明：
=
+
+
=
+
+
，
∴
=
（
+
+
）=
，
∴
∥
，
∵
与
有公共点C，
∴A1、G、C三点共线．
（2）证明：设
=
，
=
，
=
，
则|
|=|
|=|
|=a，且
•
=
•
=
•
=0，
∵
=
+
+
，
=
-
，
∴
•
=（
+
+
）•（
-
）=0，
∴
⊥
，即CA1⊥BC1，
同理可证：CA1⊥BD，
因此A1C⊥平面BC1D．
（3）解：∵
=
+
+
，
∴
2=
2+
2+
2=3a2，
即|
|=
a，因此|
|=
a．
即C到平面BC1D的距离为
a．
| CA1 |
| CB |
| BA |
| AA1 |
| CB |
| CD |
| CC1 |
∴
| CG |
| 1 |
| 3 |
| CB |
| CD |
| CC1 |
| 1 |
| 3 |
| CA1 |
∴
| CG |
| CA1 |
∵
| CG |
| CA1 |
∴A1、G、C三点共线．
（2）证明：设
| CB |
| a |
| CD |
| b |
| CC1 |
| c |
则|
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
∵
| CA1 |
| a |
| b |
| c |
| BC1 |
| c |
| a |
∴
| CA1 |
| BC1 |
| a |
| b |
| c |
| c |
| a |
∴
| CA1 |
| BC1 |
同理可证：CA1⊥BD，
因此A1C⊥平面BC1D．
（3）解：∵
| CA1 |
| a |
| b |
| c |
∴
| CA1 |
| a |
| b |
| c |
即|
| CA1 |
| 3 |
| CG |
| ||
| 3 |
即C到平面BC1D的距离为
| ||
| 3 |
点评：本题考查点共线，考查线面垂直，考查C到平面BC1D的距离，正确运用向量是关键．
练习册系列答案
相关题目
在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，D是AB中点，（直三棱柱，指侧棱垂直于底面的棱柱）．设函数f（x）=ex（sinx-cosx）（0≤x≤2011π），则函数f（x）的各极大值之和为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|