题目内容
20.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+{x}^{2}-2,x≥0}\\{lo{g}_{2}(-x)+|x|,x<0}\end{array}\right.$的零点的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 按分段函数分别讨论在各区间上的单调性及取值,从而确定零点的个数.
解答 解:当x≥0时,f(x)=2x+x2-2是增函数且连续,
f(0)=1-2<0,f(1)=2+1-2=1>0,
故f(x)在(0,1)上有且只有一个零点;
当x<0时,f(x)=log2(-x)+|x|
=log2(-x)-x是减函数且连续,
f(-1)=0+1>0,f(-$\frac{1}{3}$)=-log23$+\frac{1}{3}$<0,
故f(x)在(-1,0)上有且只有一个零点;
综上所述,函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+{x}^{2}-2,x≥0}\\{lo{g}_{2}(-x)+|x|,x<0}\end{array}\right.$的零点的个数是2,
故选:C.
点评 本题考查了分段函数的应用及函数的性质的判断与应用,同时考查了零点的判定定理的应用.

练习册系列答案
相关题目
12.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | y=tan2x | B. | y=sinx | C. | y=cos2x | D. | y=sin2x |
9.设集合A={x||x-a|<1,x∈R},B={y|y=lg(x2+1),x∈R},若A⊆B,则实数a的取值范围是( )
| A. | {a|a>1} | B. | {a|a≥1} | C. | {a|a≥-1} | D. | {a|a>-1} |
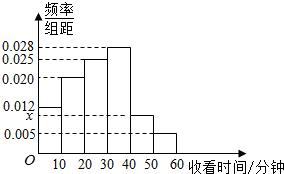 某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.
某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01. 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.