题目内容
10．已知tanα=2，计算$\frac{3sinα-cosα}{sinα+2cosα}$=$\frac{5}{4}$．分析 根据题意，利用关系式tanα=$\frac{sinα}{cosα}$将原式化简可得原式=$\frac{3tanα-1}{tanα+2}$，将tanα=2代入原式=$\frac{3tanα-1}{tanα+2}$即可得答案．
解答 解：根据题意，原式=$\frac{3sinα-cosα}{sinα+2cosα}$=$\frac{3\frac{sinα}{cosα}-\frac{cosα}{cosα}}{\frac{sinα}{cosα}+2\frac{cosα}{cosα}}$=$\frac{3tanα-1}{tanα+2}$，
而tanα=2，
则原式=$\frac{3×2-1}{2+2}$=$\frac{5}{4}$；
故答案为：$\frac{5}{4}$．
点评 本题考查同角三角函数基本关系式的运用，关键是充分利用tanα=$\frac{sinα}{cosα}$进行化简、变形．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
1．已知中心在原点，焦点在坐标轴上的双曲线的两条渐近线的夹角为$\frac{π}{3}$，则双曲线的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$或2 | D． | 2 |
18．在△ABC中，若b=2，c=6，∠A=$\frac{π}{4}$，则S△ABC=（ ）
| A． | 3$\sqrt{2}$ | B． | 4$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
5．直线x-4y+12=0在x轴和y轴的截距分别是（ ）
| A． | 12，3 | B． | -12，-3 | C． | 12，-3 | D． | -12，3 |
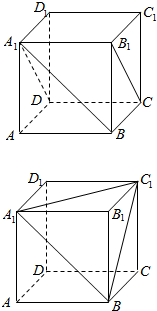正方体ABCD-A1B1C1D1中．