题目内容
9.设集合A={x||x-a|<1,x∈R},B={y|y=lg(x2+1),x∈R},若A⊆B,则实数a的取值范围是( )| A. | {a|a>1} | B. | {a|a≥1} | C. | {a|a≥-1} | D. | {a|a>-1} |
分析 化简集合A,B,利用A⊆B,即可求出实数a的取值范围.
解答 解:A={x||x-a|<1,x∈R}={x|a-1<x<a+1},B={y|y=lg(x2+1),x∈R}=[0,+∞),
∵A⊆B,
∴a-1≥0,
∴a≥1.
故选:B.
点评 本题考查集合的关系,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
1.已知中心在原点,焦点在坐标轴上的双曲线的两条渐近线的夹角为$\frac{π}{3}$,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$或2 | D. | 2 |
18.在△ABC中,若b=2,c=6,∠A=$\frac{π}{4}$,则S△ABC=( )
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
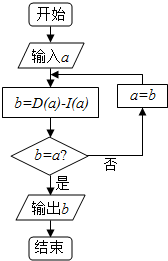 已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )