题目内容
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD.
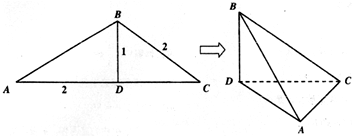
(1)求证:AC⊥平面BCD;
(2)求二面角D-AC-B的平面角的大小;
(3)求AB与平面BDC所成角的余弦值.

(1)求证:AC⊥平面BCD;
(2)求二面角D-AC-B的平面角的大小;
(3)求AB与平面BDC所成角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知中△ABC中,BD为AC边上的高,对折后,我们易得BD⊥DA,BD⊥DC,结合线面垂直的判定定理可得BD⊥平面ACD,再由线面垂直的性质,易得AC⊥BD,由余弦定理结合勾股定理可得AC⊥CD,进而可得AC⊥平面BCD;
(2)由已知中BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,结合(1)中BD⊥平面ACD,我们易得到平面BCD⊥平面ACD,AC⊥DC,进而可得AC⊥平面BCD,故∠BCD即为二面角D-AC-B的平面角;
(3)由(2)中AC⊥平面BCD,则∠ABC即为AB与平面BCD所成角,解直角三角形ABC即可求出AB与平面BCD所成角的余弦值.
(2)由已知中BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,结合(1)中BD⊥平面ACD,我们易得到平面BCD⊥平面ACD,AC⊥DC,进而可得AC⊥平面BCD,故∠BCD即为二面角D-AC-B的平面角;
(3)由(2)中AC⊥平面BCD,则∠ABC即为AB与平面BCD所成角,解直角三角形ABC即可求出AB与平面BCD所成角的余弦值.
解答:
解:(1)∵△ABC中,BD为AC边上的高
∴几何体B-ACD中,BD⊥DA,BD⊥DC,DA∩DC=D
∴BD⊥平面ACD
又∵AC?平面ACD
∴AC⊥BD;
又由BD=1,BC=AD=2,
∴CD=
,
又∵∠ADC=30°,
∴AC=
=1,
即AD2=CD2+AC2,
即AC⊥CD,
又由BD∩CD=D,
∴AC⊥平面BCD
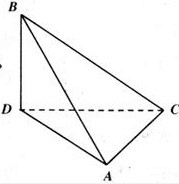
(2)由(1)中BD⊥平面ACD,BD?平面BCD
∴平面BCD⊥平面ACD
∵BD=1,BC=AD=2,使得∠ADC=30°
∴AB=
,AC=1,AC⊥DC,
又∵平面ACD∩平面BCD=CD,AC?平面ACD,
∴AC⊥平面BCD,
故∠BCD即为二面角D-AC-B的平面角,
∵BD=1,BC=2,
∴∠BCD=30°,
即二面角D-AC-B的平面角为30°.
(3)由(2)中AC⊥平面BCD,
∴∠ABC即为AB与平面BCD所成角
则cos∠ABC=
.
∴几何体B-ACD中,BD⊥DA,BD⊥DC,DA∩DC=D
∴BD⊥平面ACD
又∵AC?平面ACD
∴AC⊥BD;
又由BD=1,BC=AD=2,
∴CD=
| 3 |
又∵∠ADC=30°,
∴AC=
|
即AD2=CD2+AC2,
即AC⊥CD,
又由BD∩CD=D,
∴AC⊥平面BCD

(2)由(1)中BD⊥平面ACD,BD?平面BCD
∴平面BCD⊥平面ACD
∵BD=1,BC=AD=2,使得∠ADC=30°
∴AB=
| 5 |
又∵平面ACD∩平面BCD=CD,AC?平面ACD,
∴AC⊥平面BCD,
故∠BCD即为二面角D-AC-B的平面角,
∵BD=1,BC=2,
∴∠BCD=30°,
即二面角D-AC-B的平面角为30°.
(3)由(2)中AC⊥平面BCD,
∴∠ABC即为AB与平面BCD所成角
则cos∠ABC=
2
| ||
| 5 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面垂直的性质,其中正确理解在图形的翻折过程中,哪些直线的位置关系是不变的,进而得到相关直线垂直的有用信息是解答本题的关键.

练习册系列答案
相关题目
函数f(x)=ax-1的反函数的图象经过点(4,2),则f-1(2)的值是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、4 |
定义在R上的函数f(x),存在无数个实数x满足f(x+2)=f(x),则f(x)( )
| A、是周期为1的周期函数 |
| B、是周期为2的周期函数 |
| C、是周期为4的周期函数 |
| D、不一定是周期函数 |