题目内容
定义在R上的函数f（x），存在无数个实数x满足f（x+2）=f（x），则f（x）（ ）
| A、是周期为1的周期函数 |
| B、是周期为2的周期函数 |
| C、是周期为4的周期函数 |
| D、不一定是周期函数 |
考点：函数的周期性
专题：函数的性质及应用
分析：直接利用函数的周期的定义判断即可．
解答：
解：函数的周期的定义，是定义在R上的函数f（x），对于任意的x，恒有f（x+T）=f（x），非零常数T是周期．
本题中，x不是任意，所以函数不一定是周期函数．
故选：D．
本题中，x不是任意，所以函数不一定是周期函数．
故选：D．
点评：本题考查函数的周期的定义，基本知识的考查．
练习册系列答案
相关题目
已知a=20.5，b=lg2，c=ln2，则（ ）
| A、a＞b＞c |
| B、b＞c＞a |
| C、c＞a＞b |
| D、a＞c＞b |
已知一个算法，如图所示，则输出的结果是（ ）
| A、10 | B、11 | C、8 | D、9 |
命题“?x∈R，cosx＞0”的否定是（ ）
| A、?x∈R，cosx≤0 |
| B、?x∈R，cosx≤0 |
| C、?x∈R，cosx＞0 |
| D、?x∈R，cosx＜0 |
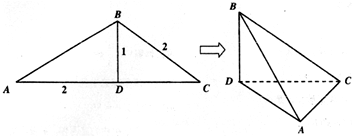
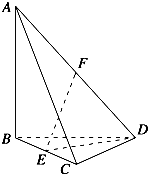如图，四面体ABCD中，AB、BC、BD两两垂直，AB=BC=BD=4，E、F分别为棱BC、AD的中点．
如图，在三棱柱A1B1C1-ABC的侧棱与底面边长都等于2，A1在底面ABC上的射影为BC的中点，则三棱柱的侧面面积为