题目内容
已知数列{an}前项n和sn=n2+4n(n∈N*),数列{bn}为等比数列,首项b1=2,公比为q(q>0),且满足b2,b3+4q,b4成等差数列.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
,记数列{cn}的前n项和为Tn,求Tn.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
| 3(an-3)•bn |
| 4 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)把当n=1时a1=s1、当n≥2时an=sn-sn-1代入sn=n2+4n(n∈N*),化简求出an,由等差中项的性质求出公比q,代入等比数列的通项公式求出bn;
(2)由(1)和条件求出cn,利用错位相减法求出数列{cn}的前n项和为Tn.
(2)由(1)和条件求出cn,利用错位相减法求出数列{cn}的前n项和为Tn.
解答:
解:(1)由题意得,sn=n2+4n(n∈N*),
当n=1时,a1=s1=5.
当n≥2时,an=sn-sn-1=n2+4n-[(n-1)2+4(n-1)]=2n+3,
验证n=1时也成立,
所以数列{an}的通项公式为:an=2n+3,
因为b2,b3+4q,b4成等差数列,b1=2.
所以2(b3+4q)=b2+b4,即q2-2q-3=0,
因为q>0,所以q=3,
所以数列{bn}的通项公式为:bn=2•3n-1…(6分)
(2)由(1)得,cn=
=n•3n,
所以Tn=1×3+2×32+3×33+…+n×3n…①
3×Tn=1×32+2×33+3×34+…+n×3n+1…②
由①-②得:-2Tn=3+32+33+34+…+3n-n×3n+1
=
-n×3n+1=
所以Tn=
…(12分)
当n=1时,a1=s1=5.
当n≥2时,an=sn-sn-1=n2+4n-[(n-1)2+4(n-1)]=2n+3,
验证n=1时也成立,
所以数列{an}的通项公式为:an=2n+3,
因为b2,b3+4q,b4成等差数列,b1=2.
所以2(b3+4q)=b2+b4,即q2-2q-3=0,
因为q>0,所以q=3,
所以数列{bn}的通项公式为:bn=2•3n-1…(6分)
(2)由(1)得,cn=
| 3(an-3)•bn |
| 4 |
所以Tn=1×3+2×32+3×33+…+n×3n…①
3×Tn=1×32+2×33+3×34+…+n×3n+1…②
由①-②得:-2Tn=3+32+33+34+…+3n-n×3n+1
=
| 3(3n-1) |
| 3-1 |
| (1-2n)•3n+1-3 |
| 2 |
所以Tn=
| (2n-1)•3n+1+3 |
| 4 |
点评:本题考查了数列中an与sn的关系式,等差中项的性质,等比数列的通项公式,以及错位相减法求数列的前n项和,考查了学生化简计算能力.

练习册系列答案
相关题目
已知sin2α=
,则cos(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知一个算法,如图所示,则输出的结果是( )


| A、10 | B、11 | C、8 | D、9 |
下列语句是命题的是( )
| A、指数函数是增函数吗 | ||
| B、若整数a是素数,则a是奇数 | ||
C、求证
| ||
| D、x>15 |
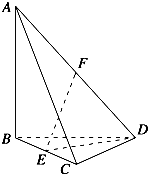 如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.
如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.