题目内容

由1、2、3、4、5、6、7、9组成的没有重复数字且1、3都不与5相邻的八位数的个数是
 
．
考点：排列、组合及简单计数问题
专题：排列组合
分析：由1、2、3、4、5、6、7、9组成的没有重复数字共有：
A
8
8
个，去掉与1，5相邻的情况有：
A
2
2
•
A
7
7
个，3，5相邻的情况有：
A
2
2
•
A
7
7
个，再加上1、3都与5相邻的八位数
A
2
2
•
A
6
6
个，可得答案．
解答： 解：由1、2、3、4、5、6、7、9组成的没有重复数字共有：
A
8
8
个，
其中1，5相邻的情况有：
A
2
2
•
A
7
7
个，
3，5相邻的情况有：
A
2
2
•
A
7
7
个，
1、3都与5相邻的八位数
A
2
2
•
A
6
6
个，
故由1、2、3、4、5、6、7、9组成的没有重复数字且1、3都不与5相邻的八位数的个数是
A
8
8
-2•
A
2
2
•
A
7
7
+
A
2
2
•
A
6
6
=21600个，
故答案为：21600
点评：本题考查的知识点是排列组合及简单计数问题，难度中档．
练习册系列答案
相关题目
如图，在△ABC中，BD为AC边上的高，BD=1，BC=AD=2，沿BD将△ABD翻折，使得∠ADC=30°，得几何体B-ACD．

（1）求证：AC⊥平面BCD；
（2）求二面角D-AC-B的平面角的大小；
（3）求AB与平面BDC所成角的余弦值．
已知四面体A-BCD的棱长都相等，Q是AD的中点，求CQ与平面DBC所成的角的正弦值．
在直角坐标系xOy中，已知点P（2，2），C（5，6）．若在以点C为圆心，r为半径的圆上存在不同的两点A，B．使得向量
PA
-2
PB
=
0
，则r的取值范围为
 
．
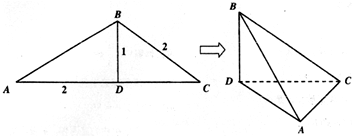
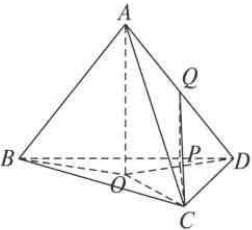
如图，在三棱柱A1B1C1-ABC的侧棱与底面边长都等于2，A1在底面ABC上的射影为BC的中点，则三棱柱的侧面面积为
 
．
已知函数f（x）=alnx+
1
2
x2-（a+1）x（a≥1）．
（1）讨论f（x）的单调性与极值点；
（2）若g（x）=
1
2
x2-x-1（x＞1），证明：当a=1时，g（x）的图象恒在f（x）的图象上方；
（3）证明：
ln2
22
+
ln3
32
+…+
lnn
n2
＜
2n2-n-1
4(n+1)
（n∈N*，n≥2）．
在直角坐标系中，四边形OPQR的顶点按逆时针顺序依次为O（0，0）、P（1，t）、Q（1-2t，2+t）、R（-2t，2），其中t∈（0，+∞），试判断四边形OPQR的形状，并给出证明．
给定函数f（x）和常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“好数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类好数对”．已知函数f（x）的定义域为[1，+∞）．
（Ⅰ）若（1，1）是函数f（x）的一个“好数对”，且f（1）=3，求f（16）；
（Ⅱ）若（2，0）是函数f（x）的一个“好数对”，且当1＜x≤2时，f（x）=
2x-x2
，求证：函数y=f（x）-x在区间（1，+∞）上无零点；
（Ⅲ）若（2，-2）是函数f（x）的一个“类好数对”，f（1）=3，且函数f（x）单调递增，比较f（x）与
x
2
+2的大小，并说明理由．
在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，E为CC1中点．求证：A1O⊥OE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网