题目内容
若
•
=|
|•|
|•cosλ＞0，求λ的取值范围．
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由条件结合
•
=|
|•|
|•cosθ（θ为两向量的夹角），再由余弦函数的性质，即可求出λ的取值范围．
| a |
| b |
| a |
| b |
解答：
解：∵
•
=|
|•|
|•cosλ＞0，又
•
=|
|•|
|•cosθ（θ为两向量的夹角）
∴cosθ=cosλ＞0，
∴2kπ≤λ＜2kπ+
或2kπ-
＜λ≤2kπ，k∈Z，
即λ的取值范围是（2kπ-
，2kπ+
），k∈Z．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴cosθ=cosλ＞0，
∴2kπ≤λ＜2kπ+
| π |
| 2 |
| π |
| 2 |
即λ的取值范围是（2kπ-
| π |
| 2 |
| π |
| 2 |
点评：本题考查向量的数量积的定义，同时考查余弦函数的图象和性质，属于基础题．
练习册系列答案
相关题目
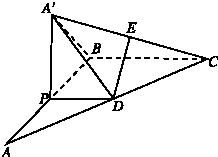如图，在△ABC中，∠B=
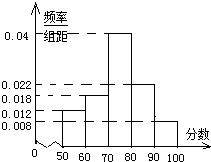某次素质测试，随机抽取了部分学生的成绩，得到如图所示的频率分布直方图．