题目内容
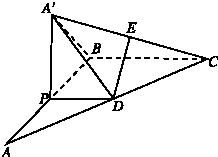 如图,在△ABC中,∠B=
如图,在△ABC中,∠B=| π |
| 2 |
(Ⅰ)若点P为AB的中点,E为A′C的中点,求证:A′B⊥DE;
(Ⅱ)当棱锥A′-PBCD的体积最大时,求PA的长.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:(Ⅰ)设F为A′B的中点,连接PF,FE,通过PDEF是平行四边形,证明A′B⊥DE;
(Ⅱ)令PA=x(0<x<2)求出体积表达式,利用导数确定函数的单调性,求出函数的最大值.
(Ⅱ)令PA=x(0<x<2)求出体积表达式,利用导数确定函数的单调性,求出函数的最大值.
解答:
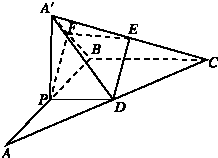 (Ⅰ)证明:如图,设F为A′B的中点,连结PF,FE.
(Ⅰ)证明:如图,设F为A′B的中点,连结PF,FE.
则有EF∥BC,EF=
BC,PD∥BC,PD=
BC,
∴DE∥PF,又A′P=PB,
∴PF⊥A′B,
故A′B⊥DE.
(Ⅱ)解:令PA=x(0<x<2),则A′P=PD=x,BP=2-x.
∵A′P⊥PD,且平面A′PD⊥平面PBCD,
∴A′P⊥平面PBCD.
∴VA′-PBCD=
Sh=
(2-x)(2+x)x=
(4x-x3).
令f(x)=
(4x-x3),
由f′(x)=
(4-3x2)=0,得x=
.
当x∈(0,
)时,f′(x)>0,f(x)单调递增;
当x∈(
,2)时,f′(x)<0,f(x)单调递减.
∴当x=
时,f(x)取得最大值,
故当VA′-PBCD最大时,PA=
.
 (Ⅰ)证明:如图,设F为A′B的中点,连结PF,FE.
(Ⅰ)证明:如图,设F为A′B的中点,连结PF,FE.则有EF∥BC,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE∥PF,又A′P=PB,
∴PF⊥A′B,
故A′B⊥DE.
(Ⅱ)解:令PA=x(0<x<2),则A′P=PD=x,BP=2-x.
∵A′P⊥PD,且平面A′PD⊥平面PBCD,
∴A′P⊥平面PBCD.
∴VA′-PBCD=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
令f(x)=
| 1 |
| 6 |
由f′(x)=
| 1 |
| 6 |
2
| ||
| 3 |
当x∈(0,
2
| ||
| 3 |
当x∈(
2
| ||
| 3 |
∴当x=
2
| ||
| 3 |
故当VA′-PBCD最大时,PA=
2
| ||
| 3 |
点评:本题是中档题,考查几何体的体积计算,函数最大值的求法,直线与直线的垂直的证明方法,考查空间想象能力,计算能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
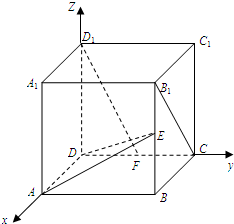 如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)
如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)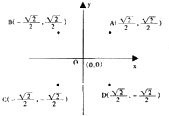 如图,A(
如图,A(