题目内容
4.设抛物线C:y2=2px(p>0)的焦点为F,点A在C上,若|AF|=$\frac{5}{2}$,以线段AF为直径的圆经过点B(0,1),则p=1或4.分析 由题意,可得A($\frac{5-p}{2}$,$\sqrt{p(5-p)}$),AB⊥BF,所以($\frac{p}{2}$,-1)•($\frac{5-p}{2}$,$\sqrt{p(5-p)}$-1)=0,即可求出p的值.
解答 解:由题意,可得A($\frac{5-p}{2}$,$\sqrt{p(5-p)}$),AB⊥BF,
∴($\frac{p}{2}$,-1)•($\frac{5-p}{2}$,$\sqrt{p(5-p)}$-1)=0,
∴$\frac{p(5-p)}{4}$-$\sqrt{p(5-p)}$+1=0,
∴p(5-p)=4,∴p=1或4.
故答案为1或4.
点评 本题考查抛物线的方程与性质,考查向量知识的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$则目标函数z=3x-4y的最大值和最小值分别为( )
| A. | -6,-8 | B. | -6,-9 | C. | -8,-9 | D. | 6,-9 |
19.已知数列{an}的前n项和Sn满足Sn+Sm=Sn+m(n,m∈N*)且a1=5,则a8=( )
| A. | 40 | B. | 35 | C. | 12 | D. | 5 |
16.平面内凸四边形有2条对角线,凸五边形有5条对角线,以此类推,凸13边形的对角线条数为( )
| A. | 42 | B. | 65 | C. | 143 | D. | 169 |
17.已知集合A={x|2x>1},B={x|0<x<1},则∁AB=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
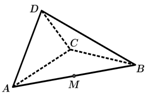 如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.
如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.