题目内容
15.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$则目标函数z=3x-4y的最大值和最小值分别为( )| A. | -6,-8 | B. | -6,-9 | C. | -8,-9 | D. | 6,-9 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x-y+2=0}\\{x+y=4}\end{array}\right.$,解得A(1,3),
联立$\left\{\begin{array}{l}{x+y=4}\\{2x-5y+10=0}\end{array}\right.$,解得B($\frac{10}{7},\frac{18}{7}$).
化目标函数z=3x-4y为y=$\frac{3}{4}x-\frac{z}{4}$,
由图可知,当直线y=$\frac{3}{4}x-\frac{z}{4}$过A时,直线在y轴上的截距最大,z有最小值为-9;
过B时,直线在y轴上的截距最小,z有最大值为-6.
∴目标函数z=3x-4y的最大值和最小值分别为-6,-9.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
5.当$x∈[-\frac{π}{3},\frac{π}{3}]$时,函数$f(x)=\sqrt{2}sin\frac{x}{4}cos\frac{x}{4}+\sqrt{6}{cos^2}\frac{x}{4}-\frac{{\sqrt{6}}}{2}$的最小值为( )
| A. | $-\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
6.已知R上的奇函数f(x)满足:当x>0时,f(x)=x2+x-1,则f[f(-1)]=( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
10.某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
(1)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级编号为4的3件产品记为x1,x2,x3,等级编号为5的2件产品记为y1,y2,现从x1,x2,x3,y1,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为x1,x2,x3,等级编号为5的2件产品记为y1,y2,现从x1,x2,x3,y1,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
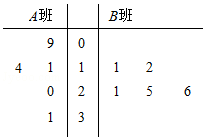 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字). 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )