题目内容
14.已知数列{an}是各项均不为零的等差数列,Sn为其前n项和,且S2n-1=a${\;}_{n}^{2}$(n∈N*),若不等式$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$≤nlog${\;}_{\frac{1}{8}}$λ对任意n∈N*恒成立,则实数λ的最大值是$\frac{1}{2}$.分析 数列{an}是各项均不为零的等差数列,设公差为d,又S2n-1=a${\;}_{n}^{2}$(n∈N*),n=1时,${a}_{1}={a}_{1}^{2}$,解得a1.n=2时,S3=${a}_{2}^{2}$,解得d.可得an=2n-1.利用“裂项求和”方法可得:$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{n}{2n+1}$.代入不等式$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$≤nlog${\;}_{\frac{1}{8}}$λ,化简利用数列的单调性、对数函数的单调性即可得出.
解答 解:∵数列{an}是各项均不为零的等差数列,设公差为d,又S2n-1=a${\;}_{n}^{2}$(n∈N*),
∴n=1时,${a}_{1}={a}_{1}^{2}$,解得a1=1.
n=2时,S3=${a}_{2}^{2}$,即3+3d=(1+d)2,解得d=2或d=-1(舍去).
∴an=1+2(n-1)=2n-1.
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$=$\frac{n}{2n+1}$.
不等式$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$≤nlog${\;}_{\frac{1}{8}}$λ,即:$\frac{n}{2n+1}$≤nlog${\;}_{\frac{1}{8}}$λ,化为:log${\;}_{\frac{1}{8}}$λ≥$\frac{1}{2n+1}$.
不等式$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{{a}_{2}a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$≤nlog${\;}_{\frac{1}{8}}$λ对任意n∈N*恒成立,∴log${\;}_{\frac{1}{8}}$λ≥$\frac{1}{3}$,∴0<λ≤$(\frac{1}{8})^{\frac{1}{3}}$=$\frac{1}{2}$.
则实数λ的最大值是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了数列递推关系、等差数列的通项公式、“裂项求和”方法、数列的单调性、对数函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | $-\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
| A. | $\frac{1}{5}+\frac{3}{5}i$ | B. | $\frac{1}{5}-\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $-\frac{1}{5}-\frac{3}{5}i$ |
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
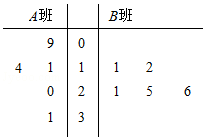 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).