题目内容
9.若等比数列{an}的公比为2,且a3-a1=6,则$\frac{1}{{{a}_{1}}}$+$\frac{1}{{{a}_{2}}}$+…+$\frac{1}{{{a}_{n}}}$=1-$\frac{1}{{2}^{n}}$.分析 等比数列{an}的公比为2,且a3-a1=6,可得a1(22-1)=6,解得a1.可得an=2n.再利用等比数列的求和公式即可得出.
解答 解:等比数列{an}的公比为2,且a3-a1=6,
∴a1(22-1)=6,解得a1=2.
∴an=2n.
则$\frac{1}{{{a}_{1}}}$+$\frac{1}{{{a}_{2}}}$+…+$\frac{1}{{{a}_{n}}}$=$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$.
故答案为:1-$\frac{1}{{2}^{n}}$.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知复数z满足(2-i)z=1+i(i为虚数单位),则$\overline z$=( )
| A. | $\frac{1}{5}+\frac{3}{5}i$ | B. | $\frac{1}{5}-\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $-\frac{1}{5}-\frac{3}{5}i$ |
17.已知复数z满足z(1-i)2=1+i(i为虚数单位),则z=( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
14.已知复数z,满足(z-1)i=i-1,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2+i | D. | $\sqrt{5}$ |
2.函数y=kx+2与函数$y=\frac{1}{|x|}$的图象至少有两个公共点,关于k不等式(k-2)a-k>0有解,则实数a的取值范围是( )
| A. | $-1<a<\frac{1}{3}$ | B. | $a<\frac{1}{3}$ | C. | a<-1 | D. | a≥1 |
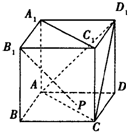 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.