题目内容
某人午觉醒来,发现表停了,他打开收音机,想听电台报时(电台每隔一小时报一次时),求他等待的时间不多于10分钟的概率.
考点:几何概型
专题:概率与统计
分析:由电台整点报时的时刻是任意的知这是一个几何概型,电台整点报时知事件总数包含的时间长度是60,而他等待的时间不多于10分钟的事件包含的时间长度是10,两值一比即可求出所求.
解答:
解:设A={等待的时间不多于10分钟}…(3分)
事件A恰好是打开收音机的时刻位于[50,60]时间段内,
因此由几何概型的求概率的公式可得p(A)=
=
…(8分)
即“等待报时的时间不超过10分钟”的概率为
…(10分)
事件A恰好是打开收音机的时刻位于[50,60]时间段内,
因此由几何概型的求概率的公式可得p(A)=
| 60-50 |
| 60 |
| 1 |
| 6 |
即“等待报时的时间不超过10分钟”的概率为
| 1 |
| 6 |
点评:本题主要考查了几何概型,本题先要判断该概率模型,对于几何概型,它的结果要通过长度、面积或体积之比来得到,属于中档题.

练习册系列答案
相关题目
如果函数f(x)=(
)|x|(-∞<x<+∞),那么函数f(x)是( )
| 1 |
| 2 |
| A、奇函数,且在(-∞,0)上是增函数 |
| B、偶函数,且在(-∞,0)上是减函数 |
| C、奇函数,且在(0,+∞)上是增函数 |
| D、偶函数,且在(0,+∞)上是减函数 |
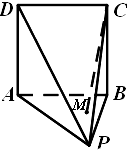 如图,四棱锥P-ABCD的底面ABCD是边长为1的正方形,面PAB⊥面ABCD.在面PAB内的有一个动点M,记M到面PAD的距离为d.若|MC|2-d2=1,则动点M在面PAB内的轨迹是( )
如图,四棱锥P-ABCD的底面ABCD是边长为1的正方形,面PAB⊥面ABCD.在面PAB内的有一个动点M,记M到面PAD的距离为d.若|MC|2-d2=1,则动点M在面PAB内的轨迹是( )| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
函数f(x)=7+ax-3(a>0,a≠1)的图象恒过定点P,则定点P的坐标是( )
| A、(3,3) |
| B、(3,2) |
| C、(3,8) |
| D、(3,7) |
