题目内容
13.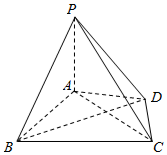 已知四棱锥P一ABCD,如图所示,其中平面PAD⊥平面ABCD,PA⊥AD,PA=AB=BC=AC=4,线段AC被线段BD平分.
已知四棱锥P一ABCD,如图所示,其中平面PAD⊥平面ABCD,PA⊥AD,PA=AB=BC=AC=4,线段AC被线段BD平分.(I)求证:BD⊥平面PAC;
(Ⅱ)若∠ACD=30°,求二面角A-PC-B的余弦值.
分析 (I)根据面面垂直的性质定理结合线面垂直的判定定理即可证明BD⊥平面PAC;
(Ⅱ)根据二面角的定义作出二面角的平面角,即可求二面角A-PC-B的余弦值.
解答  证明:(I)∵平面PAD⊥平面ABCD,PA⊥AD,
证明:(I)∵平面PAD⊥平面ABCD,PA⊥AD,
∴PA⊥平面ABCD,
∵BD?平面ABCD,
∴PA⊥BD,
∵AB=BC=AC=4,线段AC被线段BD平分,
∴BD⊥AC,
∵AC∩PA=A,
∴BD⊥平面PAC;
(Ⅱ)由(I)得BD⊥平面PAC,
则过E作EF⊥PC于F,连接BF,
则BF⊥PC,
即∠EFB是二面角A-PC-B的平面角,
∵AB=BC=AC=4,线段AC被线段BD平分,
∴CE=2,BE=2$\sqrt{3}$,
∵PA=AC=4,
∴∠PCA=45°,
则EF=CFcos45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
则BF=$\sqrt{B{E}^{2}+E{F}^{2}}$=$\sqrt{14}$,
即cos∠EFB=$\frac{EF}{BF}$=$\frac{\sqrt{2}}{\sqrt{14}}$=$\frac{\sqrt{7}}{7}$,
即二面角A-PC-B的余弦值是$\frac{\sqrt{7}}{7}$.
点评 本题主要考查面面垂直和线面垂直的判断以及二面角的求解,利用二面角平面角的定义作出二面角的平面角是解决本题的关键.本题也可以使用向量法进行求解.

练习册系列答案
相关题目
1.圆(x+1)2+(y+2)2=4与圆(x-2)2+(y-2)2=9的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
18.在递增的等差数列{an}中,a1+a5=1,a2a4=-12,则公差d为( )
| A. | $\frac{7}{2}$ | B. | -$\frac{7}{2}$ | C. | $\frac{7}{2}$或-$\frac{7}{2}$ | D. | 7或-7 |
2.在如图程序框图中,输入n=l,按程序运行后输出的结果为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

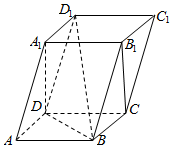 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.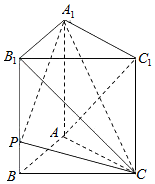 如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.
如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.