题目内容
3．在△ABC中，若$\frac{sinA+sinB+sinC}{cosA+cosB+cosC}$=$\sqrt{3}$，则（2cosA-1）（2cosB-1）（2cosC-1）=0．分析 先根据等比性质求出A=B=C=60°，再代值计算即可．
解答 解：在△ABC中，根据等比性质，$\frac{sinA+sinB+sinC}{cosA+cosB+cosC}$=$\sqrt{3}$=tanA=tanB=tanC，
∴A=B=C=60°，
∴（2cosA-1）（2cosB-1）（2cosC-1）=（2×$\frac{1}{2}$-1）（2×$\frac{1}{2}$-1）（2×$\frac{1}{2}$-1）=0，
故答案为：0．
点评 本题考查了等比性质三角函数的化简，属于基础题．
练习册系列答案
相关题目
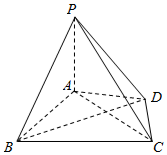已知四棱锥P一ABCD，如图所示，其中平面PAD⊥平面ABCD，PA⊥AD，PA=AB=BC=AC=4，线段AC被线段BD平分．
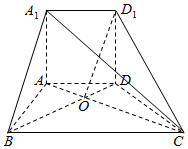如图所示的一个几何体A1D1-ABCD中，底面ABCD为一个等腰梯形，AD∥BC且AD=$\sqrt{2}$，BC=2$\sqrt{2}$，对角线AC⊥BD，且交于点O，正方形ADD1A1垂直于底面ABCD．
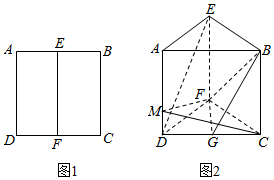如图1，在边长为4的正方形ABCD中，E、F分别是AB、CD的中点，沿EF将矩形ADFE折起使得二面角A-EF-C的大小为90°（如图2），点G是CD的中点