题目内容
18．在递增的等差数列{an}中，a1+a5=1，a2a4=-12，则公差d为（ ）| A． | $\frac{7}{2}$ | B． | -$\frac{7}{2}$ | C． | $\frac{7}{2}$或-$\frac{7}{2}$ | D． | 7或-7 |
分析 由题意列关于首项和公差的方程组，求解方程组得答案．
解答 解：∵数列{an}为等差数列，且a1+a5=1，a2a4=-12，
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}+4d=1}\\{（{a}_{1}+d）（{a}_{1}+3d）=-12}\end{array}\right.$，即$\left\{\begin{array}{l}{2{a}_{1}+4d=1}\\{（{a}_{1}+d）（{a}_{1}+3d）=-12}\end{array}\right.$，
解得：$d=-\frac{7}{2}$，或d=$\frac{7}{2}$．
∵数列为递增数列，∴d=$\frac{7}{2}$．
故选：A．
点评 本题考查等差数列的通项公式，考查方程组的解法，是基础的计算题．
练习册系列答案
相关题目
8．P为△ABC内部一点，且满足|PB|=2|PA|=2，$∠APB=\frac{5π}{6}$，且$2\overrightarrow{PA}+3\overrightarrow{PB}+4\overrightarrow{PC}=\overrightarrow 0$，则△ABC的面积为（ ）
| A． | $\frac{9}{8}$ | B． | $\frac{4}{3}$ | C． | 1 | D． | $\frac{6}{5}$ |
如图是计算1+3+5+…+99的程序框图，
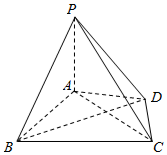已知四棱锥P一ABCD，如图所示，其中平面PAD⊥平面ABCD，PA⊥AD，PA=AB=BC=AC=4，线段AC被线段BD平分．