题目内容
设函数f(x)=|x+1|+|x-5|,x∈R.
(1)求不等式f(x)<x+10的解集;
(2)如果关于x的不等式f(x)≥a-(x-2)2在R上恒成立,求实数a的取值范围.
(1)求不等式f(x)<x+10的解集;
(2)如果关于x的不等式f(x)≥a-(x-2)2在R上恒成立,求实数a的取值范围.
考点:带绝对值的函数
专题:不等式
分析:(1)去掉绝对值,化简f(x),求出不等式f(x)<x+10的解集;
(2)设g(x)=a-(x-2)2,求出g(x)max与f(x)min;由f(x)≥g(x)在R上恒成立,得f(x)min≥g(x)max,求出a的取值范围.
(2)设g(x)=a-(x-2)2,求出g(x)max与f(x)min;由f(x)≥g(x)在R上恒成立,得f(x)min≥g(x)max,求出a的取值范围.
解答:
解:(1)去掉绝对值,f(x)=
;
当x<-1时,由-2x+4≤x+10,解得x≥-2,∴-2≤x<-1;
当-1≤x<5时,由6≤x+10,解得x≥-4,∴-1≤x<5;
当x≥5时,由2x-4≤x+10,解得x≤14,∴5≤x≤14;
综上,不等式的解集为[-2,14];---(5分)
(2)设g(x)=a-(x-2)2,则g(x)max=g(2)=a,
而f(x)=|x+1|+|x-5|≥|(x+1)-(x-5)|=6,即f(x)min=6;
∴f(x)≥g(x)在R上恒成立时,应满足f(x)min≥g(x)max,
∴a≤6;即a的取值范围是{a|a≤6}.---(10分)
|
当x<-1时,由-2x+4≤x+10,解得x≥-2,∴-2≤x<-1;
当-1≤x<5时,由6≤x+10,解得x≥-4,∴-1≤x<5;
当x≥5时,由2x-4≤x+10,解得x≤14,∴5≤x≤14;
综上,不等式的解集为[-2,14];---(5分)
(2)设g(x)=a-(x-2)2,则g(x)max=g(2)=a,
而f(x)=|x+1|+|x-5|≥|(x+1)-(x-5)|=6,即f(x)min=6;
∴f(x)≥g(x)在R上恒成立时,应满足f(x)min≥g(x)max,
∴a≤6;即a的取值范围是{a|a≤6}.---(10分)
点评:本题考查了含有绝对值不等式的解法与应用问题,也考查了函数恒成立问题,解题时应根据题意,化含有绝对值的函数为分段函数,是中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
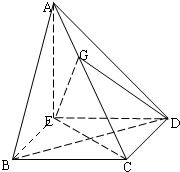 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6