题目内容

14．曲线C的参数方程为$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=si{n}^{2}θ}\end{array}\right.$（θ是参数），则曲线C的形状是（　　）
A．线段B．直线C．射线D．圆

分析 曲线C的参数方程消去参数，能求出普通方程，由经能判断曲线C的形状．

解答 解：∵曲线C的参数方程为$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=si{n}^{2}θ}\end{array}\right.$（θ是参数），
∴x=2+y，即x-y-2=0，且0≤y≤1，2≤x≤3．
∴曲线C的形状是线段．
故选：A．

点评 本题考查曲线的形状的判断，考查参数方程、直角坐标方程的互化等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．

练习册系列答案
相关题目
4．若曲线C的参数方程为$\left\{{\begin{array}{l}{x=-1+\frac{1}{2}t}\\{y=2+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$（t为参数），则下列说法正确的是（　　）
A．曲线C是直线且过点（-1，2）B．曲线C是直线且斜率为$\frac{{\sqrt{3}}}{3}$
C．曲线C是圆且圆心为（-1，2）D．曲线C是圆且半径为|t|
5．为了了解某校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组
的频率之比为1：2：3，第1小组的频数为6，则报考飞行员的学生人数是（　　）
A．32B．40C．48D．56
2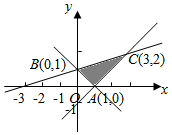．设x，y满足如图所示的可行域（阴影部分），则$z=\frac{1}{2}x-y$的最大值为（　　）
A．$\frac{1}{2}$B．0C．$-\frac{1}{2}$D．-1
9．已知函数f（x）=alnx-x2．
（1）当a=2时，求函数y=f（x）在[$\frac{1}{2}$，2]上的最大值；
（2）令g（x）=f（x）+ax，若y=g（x））在区间（0，3）上为单调递增函数，求a的取值范围；
（3）当a=2时，函数h（x）=f（x）-mx的图象与x轴交于两点A（x1，0），B（x2，0），且0＜x1＜x2，又h′（x）是h（x）的导函数．若正常数α，β满足条件α+β=1，β≥α．试比较h'（αx1+βx2）与0的关系，并给出理由．
19．已知f（x）=2x2+bx+c，不等式f（x）＜0的解集为（0，5）．
（1）求b，c的值；
（2）若对任意x∈[-1，1]，不等式f（x）+t≤2恒成立，求t的取值范围．
6．在期中考试中，高三某班50名学生化学成绩的平均分为85分、方差为8.2，该班某位同学知道自己的化学成绩为95，则下列四个数中不可能是该班化学成绩的是（　　）
A．65B．75C．90D．100
14．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的短轴长为2，焦距是短轴的$\sqrt{2}$倍．
（1）求椭圆的方程；
（2）若直线y=kx+2（ k≠0）与椭圆交于C、D两点，|CD|=$\frac{{6\sqrt{2}}}{5}$，求k的值．
15．若实数a，b满足$\frac{1}{a^2}+\frac{1}{b^2}=ab$，则ab的最小值为（　　）
A．1B．$\sqrt{2}$C．2D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网