题目内容
10.设抛物线y2=2px(p>0)的焦点为F,点A(0,-2),若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为$\frac{3\sqrt{2}}{4}$.分析 根据抛物线方程可表示出焦点F的坐标,进而求得B点的坐标代入抛物线方程求得p,则B点坐标和抛物线准线方程可求,进而求得B到该抛物线准线的距离.
解答 解:依题意可知F坐标为($\frac{p}{2}$,0)
∴B的坐标为($\frac{p}{4}$,-1)代入抛物线方程得$\frac{{p}^{2}}{2}$=1,解得p=$\sqrt{2}$,
∴抛物线准线方程为x=-$\frac{\sqrt{2}}{2}$
所以点B到抛物线准线的距离为$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{4}$,
故答案为:$\frac{3\sqrt{2}}{4}$.
点评 本题主要考查抛物线的定义及几何性质,考查计算能力.

练习册系列答案
相关题目
20.执行如图所示的程序框图,输出n的值为( )


| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
1.六个人站成一排照相,要求甲、乙、丙3人有且只有两人相邻,则不同的站法种数有( )
| A. | 18 | B. | 108 | C. | 216 | D. | 432 |
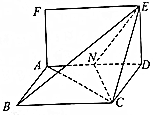 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.