题目内容
14.在矩形ABCD中,E、F分别为AB、BC的中点,记△DEF三边及内部组成的区域为Ω,$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,当点P在Ω上运动时,2x+3y的最大值为$\frac{7}{2}$.分析 以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,不妨设AB=2a,AD=2b,根据向量的坐标运算可得m=2ax,n=2by,再根据线性规划求出最大值.
解答 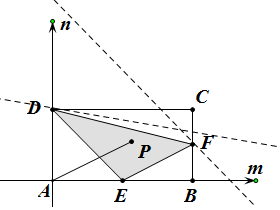 解:以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,
解:以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,
不妨设AB=2a,AD=2b,
则A(0,0),B(2a,0),D(0,2b),
∵E、F分别为AB、BC的中点,
∴E(a,0),F(2a,b),
再设P(m,n),则0≤m≤2a,0≤n≤2b,
∵$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,
∴(m,n)=x(2a,0)+y(0,2b)=(2ax,2by),
∴m=2ax,n=2by,
∴设z=2x+3y=$\frac{m}{a}$+$\frac{3n}{2b}$,
∴n=-$\frac{2b}{3a}$m+$\frac{2b}{3}$z,
平移直线n=-$\frac{2b}{3a}$m+$\frac{2b}{3}$z,当与y轴上的截距最大时,此时z最大,
若经过点F(2a,b)时,最大,此时z=2a×$\frac{1}{a}$+$\frac{3}{2b}$×b=$\frac{7}{2}$,
若经过点D(0,b)时,最大,此时z=0×$\frac{1}{a}$+$\frac{3}{2b}$×2b=3,
综上所述2x+3y的最大值为$\frac{7}{2}$,
故答案为:$\frac{7}{2}$.
点评 本题考查了向量的坐标运算和和线性规划的问题,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.抛物线y2=2px的焦点为F,点A、B、C在此抛物线上,点A坐标为(1,2).若点F恰为△ABC的重心,则直线BC的方程为( )
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
3.函数y=xsinx(x∈[-π,π])的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
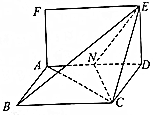 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.