题目内容
17.下列结论中正确的是②④.①$sin{750°}=\frac{{\sqrt{3}}}{2}$.
②如果随机变量ξ~$B(20,\frac{1}{2})$,那么D(ξ)为5.
③如果命题“?(p∨q)”为假命题,则p,q均为真命题.
④已知圆 x2+y2+2x-4y+1=0关于直线 2ax-by+2=0(a,b∈R)对称,则ab$≤\frac{1}{4}$.
分析 ①,sin750°=sin(7200+300)=sin30°=$\frac{1}{2}$.
②,如果随机变量ξ~$B(20,\frac{1}{2})$,那么D(ξ)=20×$\frac{1}{2}×(1-\frac{1}{2})$=5;
③,如果命题“?(p∨q)”为假命题,则p∨q真命题.p,q至少一个为真命题;
④,已知圆 x2+y2+2x-4y+1=0关于直线 2ax-by+2=0(a,b∈R)对称,则直线过圆心,即a+b=1,1=a2+b2+2ab≥4ab,则ab$≤\frac{1}{4}$;
解答 解:对于①,sin750°=sin(7200+300)=sin30°=$\frac{1}{2}$,故错.
对于②,如果随机变量ξ~$B(20,\frac{1}{2})$,那么D(ξ)=20×$\frac{1}{2}×(1-\frac{1}{2})$=5.故正确;
对于③,如果命题“?(p∨q)”为假命题,则p∨q真命题.p,q至少一个为真命题,故错;
对于④,已知圆 x2+y2+2x-4y+1=0关于直线 2ax-by+2=0(a,b∈R)对称,则直线过圆心,即a+b=1,1=a2+b2+2ab≥4ab,则ab$≤\frac{1}{4}$.故正确;
故答案为:②④
点评 本题考查了命题真假判定,涉及到了大量的基础知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知集合A={x∈R|-2≤x≤5},B={x∈R|x2<9},则A∪B等于( )
| A. | [-2,3) | B. | [3,5] | C. | (-3,5] | D. | (-∞,-3)∪[-2,+∞) |
12.某校开展研究性学习活动需组成指导教师团队,决定用分层抽样的方法从高一、高二、高三三个年级相关教师中抽取,有关数据如下表:(单位:人)
(Ⅰ)求x、y;
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.
| 年级 | 相关教师数 | 抽取教师数 |
| 高一 | x | 4 |
| 高二 | 12 | 2 |
| 高三 | 18 | y |
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.
9.抛物线y2=2px的焦点为F,点A、B、C在此抛物线上,点A坐标为(1,2).若点F恰为△ABC的重心,则直线BC的方程为( )
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
7.设全集U=R,集合A={y|y=3-x2},B={x|y=log2(x+2)},则(∁UA)∩B=( )
| A. | {x|-2<x≤3} | B. | {x|x>3} | C. | {x|x≥3} | D. | {x|x<-2} |
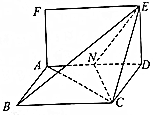 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.